one
In tensorflow, exponential decay method is provided to solve the problem of setting learning rate.
adopt tf.train.exponential_ The decay function realizes the exponential decay learning rate.
Steps: 1. First, use a larger learning rate (purpose: to get a better solution quickly);
Secondly, the learning rate is gradually reduced by iteration;
Code implementation:
[html]
view plain
copy
decayed_ learning_ rate=learining_ rate*decay_ rate^(global_ step/decay_ steps)
Among them, decayed_ learning_ Rate is the learning rate used in each round of optimization;
learning_ Rate is the preset initial learning rate;
decay_ Rate is the attenuation coefficient;
decay_ Steps is the decay rate.
and tf.train.exponential_ For the decay function, you can use the stair case (the default value is false; when it is true, the global_ step/decay_ Steps) are converted to integers, and different attenuation methods are selected.
Code example:
[html]
view plain
copy
global_ step = tf.Variable (0) learning_ rate = tf.train.exponential_ decay(0.1, global_ Step, 100, 0.96, stair case = true) # generating learning rate # learning_ step = tf.train.GradientDescentOptimizer (learning_ rate).minimize(….., global_ step=global_ Step) # use exponential decay learning rate
learning_ Rate: 0.1; stair case = true; then multiply by 0.96 after every 100 rounds of training
Generally, the setting of initial learning rate, attenuation coefficient and attenuation speed is subjective (i.e. empirical setting), while the decreasing speed of loss function is not necessarily related to the loss after iteration,
So the effect of neural network can’t be compared by the falling speed of loss function in previous rounds.
two
tf.train.exponential_ decay(learning_ rate, global_ , decay_ steps, decay_ rate, staircase=True/False)
For example:
[python]
view plain
copy
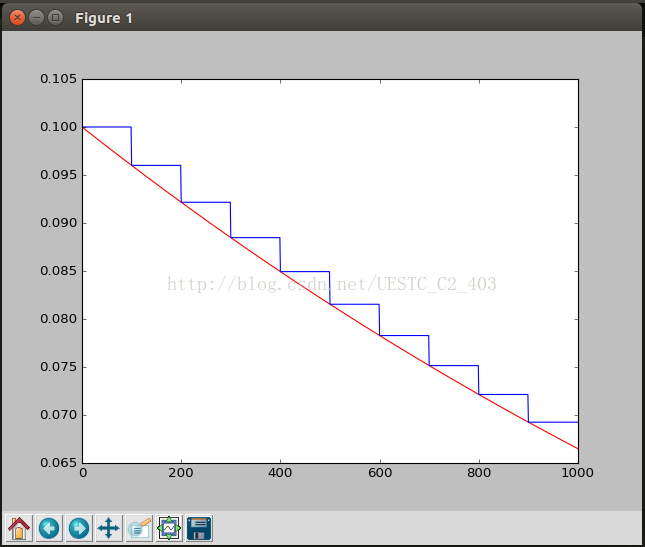
import tensorflow as tf; import numpy as np; import matplotlib.pyplot as plt; learning_ rate = 0.1 decay_ rate = 0.96 global_ steps = 1000 decay_ steps = 100 global_ = tf.Variable ( tf.constant (0)) c = tf.train.exponential_ decay(learning_ rate, global_ , decay_ steps, decay_ rate, staircase=True) d = tf.train.exponential_ decay(learning_ rate, global_ , decay_ steps, decay_ rate, staircase=False) T_ C = [] F_ D = [] with tf.Session () as sess: for i in range(global_ steps): T_ c = sess.run (c,feed_ dict={global_ : i}) T_ C.append(T_ c) F_ d = sess.run (d,feed_ dict={global_ : i}) F_ D.append(F_ d) plt.figure (1) plt.plot (range(global_ steps), F_ D, ‘r-‘) plt.plot (range(global_ steps), T_ C, ‘b-‘) plt.show ()
Analysis:
The initial learning rate is 0.1, and the total number of iterations is 1000. If stair case = true, it means every decade_ Steps calculates the change of learning rate and updates the original learning rate. If it is false, it means that each step updates the learning rate. Red means false and green means true.
results: