Tag Archives: matlab

[Solved] Vivado System Generator for DSP: “Error evaluating ‘OpenFcn‘ callback of Xilinx Block“

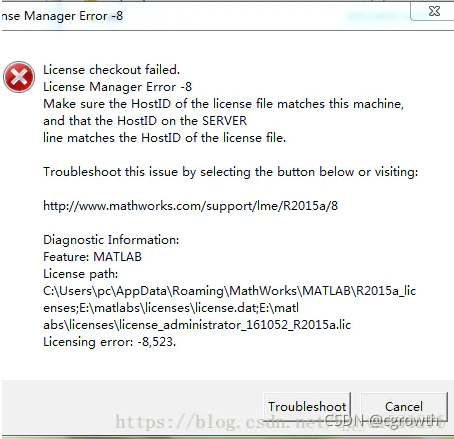
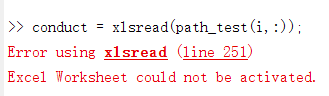
When using Vivado System Generator for DSP, I encountered the error “Error evaluating ‘OpenFcn’ callback of Xilinx Block”, the solution is as follows.

1 check whether the installed System Generator and Matlab version match, I use Matlab2019b + Vivado19.2 version, the specific installation method of the expansion package see Baidu.

2 check whether it is opened from System Generator, the software will automatically open Matlab, no additional separate open Matlab software, Matlab will open the following content.

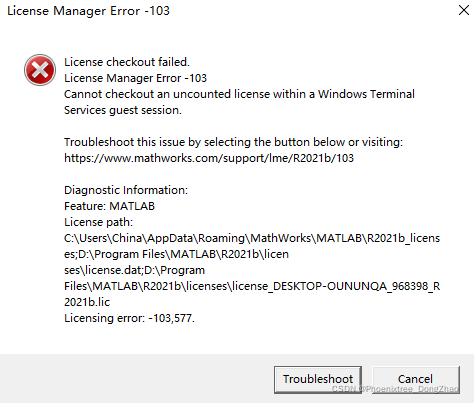
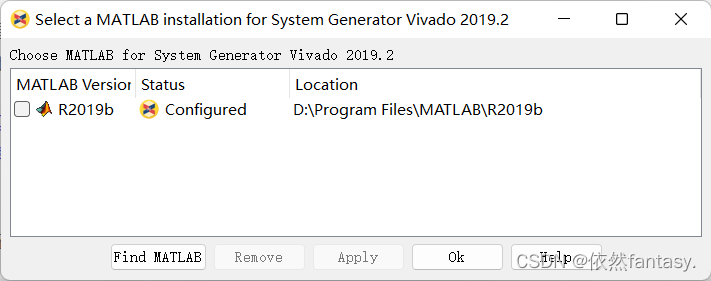
3 If the above error still occurs, open System Generator 20xx.x MATLAB Configurator software,

The following interface pops up. After checking MATLAB, remove, close and reapply;

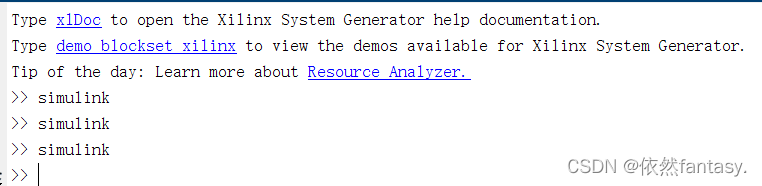
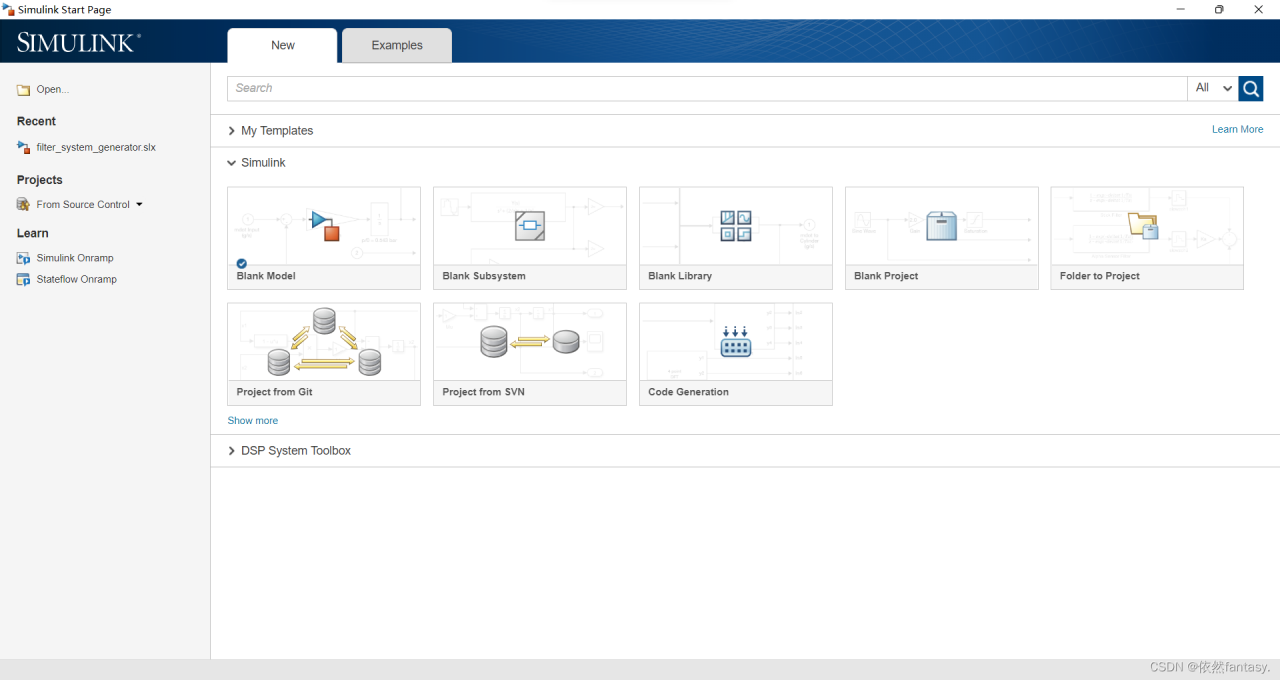
4 Input simulink in MATLAB,

The following interface appears, and select Blank Model;

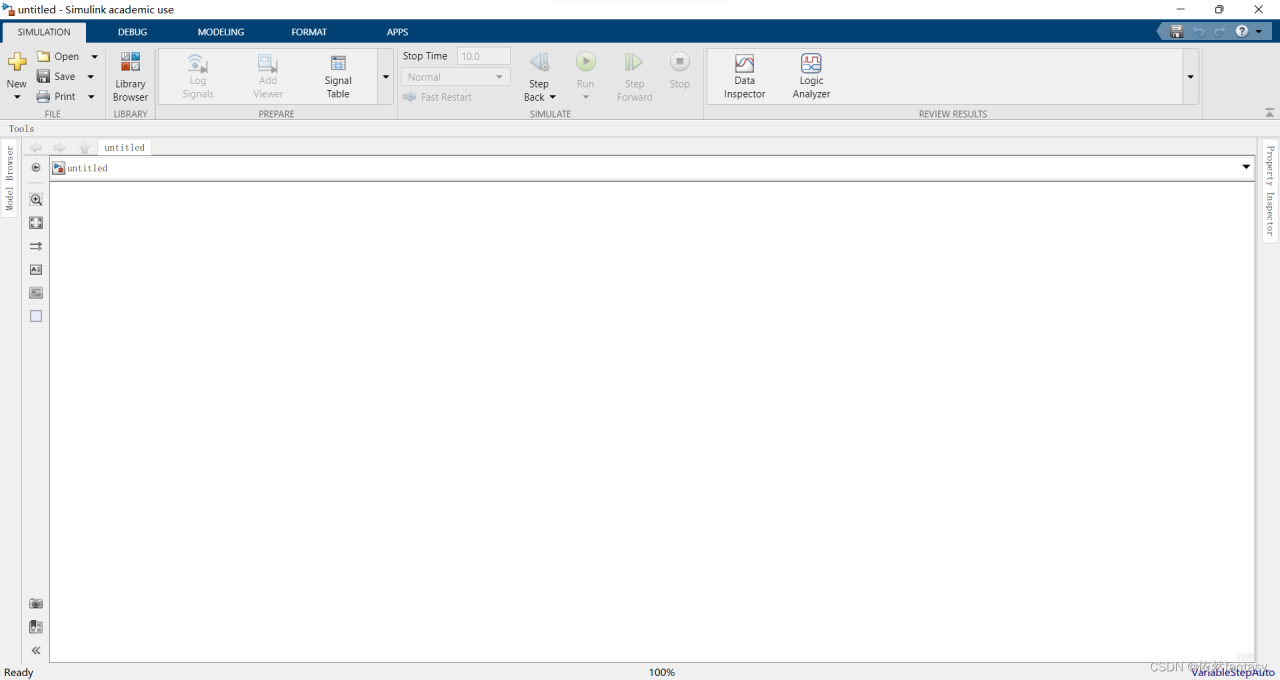
5 Click Library Browser,

Find xilinx blockset, and the corresponding option appears,

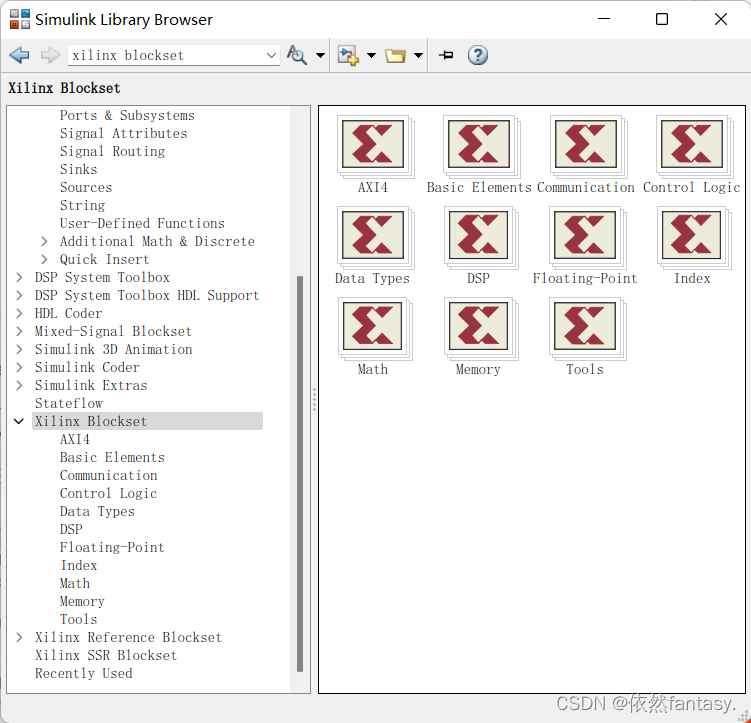
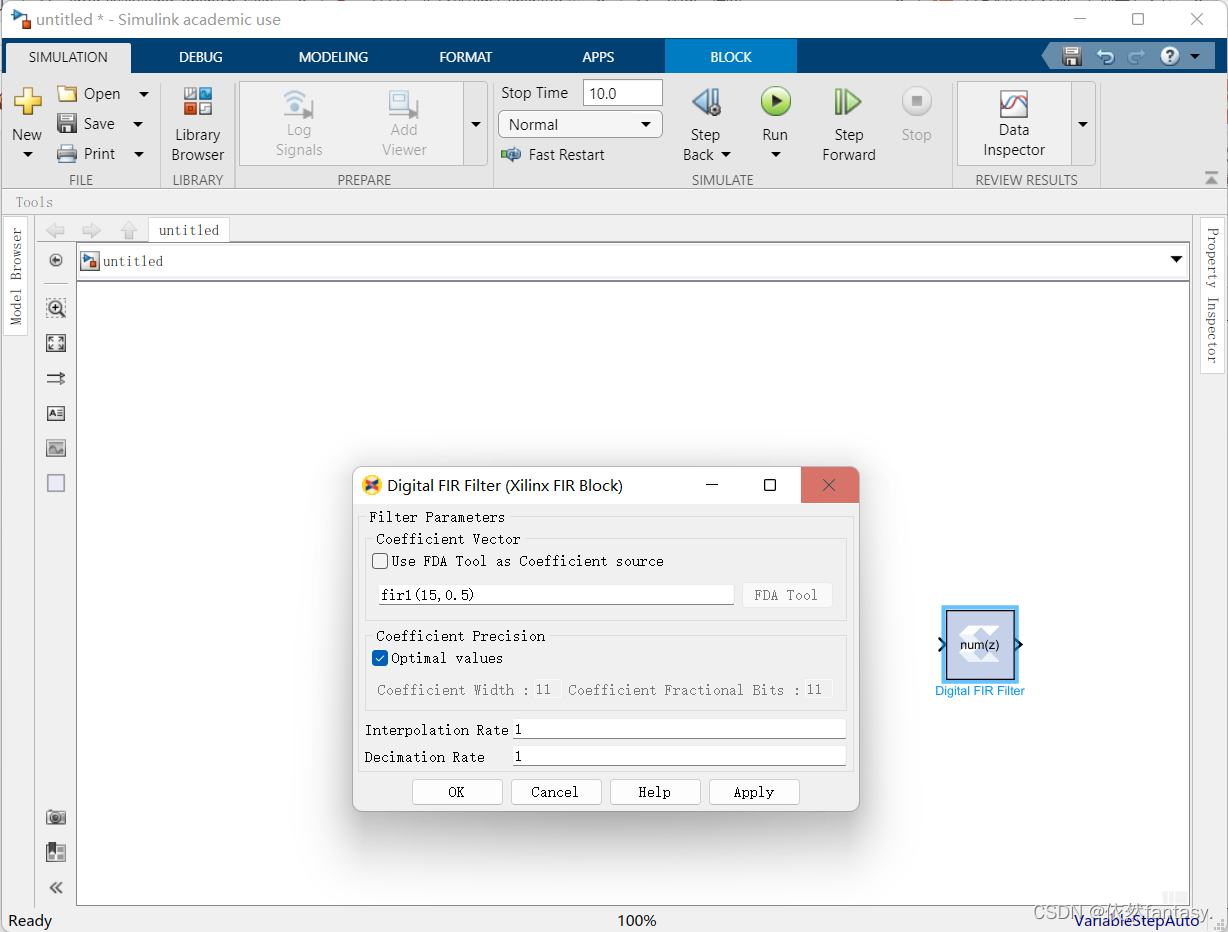
Add a module, the parameter configuration dialog box appears, and the problem is solved!

How to Solve m_gshhs_i Error

I encountered a small problem when running m_gshhs_i after installing High Precision Shoreline GSHHS

First, review the installation method:

Step1:
Download GSHHS coastlines and WDBII rivers/borders in native binary format （ zip archive ）‘gshhs+wdbii_2.2.0.zip’ from http://www.soest.Hawaii.edu/pwessel/gshhs/

Step 2:
unzip the zip file to the (……\MATLAB\toolbox\m_map\private) path

If there is no problem using m_gshhs_i in matlab after the above two steps, then there is no need to perform the operation and just use it normally. If the error is reported using m_gshhs_i as follows.

WARNING: Coastline file private/gshhs_i.b not found \n(Have you installed it?See the M_Map User's Guide for details)\n ---Using default coastline instead

Then we need to go to ……\MATLAB\toolbox\m_map\path to find the m_gshhs.m file, open it and find

FILNAME='private/gshhs_i.b';

Modify it with:

FILNAME='private\';

After saving, use m_gshhs_i again and find that it works fine. If it does not work properly after modification, then try modifying it to

FILNAME='The path to matlab on your computer\MATLAB\toolbox\m_map\private\';

At this time, it can be used normally m_gshhs_i.

[Solved] Matlab 2021b install activate Error: License manager error – 103

Error reporting:

Firstly, this error is not a problem with the installation or activation of MATLAB. Secondly, this occurs only when the remote desktop uses MATLAB.

Cause analysis:

This is because matlab uses FLEXlm for license management, while FLEXlm does not support remote desktop access. However, you can use the license file with a little modification.

(reprint the solution of the license manager error – 103 reported by MATLAB on the remote desktop)

Solution:

1. Enter the license file under r2021b\licenses:

2. Open with Notepad:

3. Ctrl + H enters the replacement window and replaces’ sign = ‘with’ ts’_OK SIGN=’：

After modification, save.

Directly open matlab again, you can succeed!

Matlab 2018a Error: License Manager Error-8 [Solved]

How to Solve the license manager error-8 problem in MATLAB 2018a

After confirming that all files in the crack file have been copied to the installation file of MATLAB. The MATLAB shortcut cannot be started after clicking on the desktop. Delete the shortcut of the desktop and enter matlab.com under the bin directory file of the installation file Exe file to start.

[Solved] Ubuntu 20.04 install MATLAB and toolbox permissions Error

1. Prompt for no access during installation
open the install file with sudo command, and remember to CD to the install directory

 sudo ./install

if the program is stuck and cannot be opened after entering the password, open the terminal and enter the following command

xhost +SI:localuser:root

2. Prompt for no access when installing the toolbox using the built-in add on
use Chmod to adjust file access rights

sudo chmod -R o+rw /usr/local/MATLAB/RXXXXx

after adjusting the permissions, you can download it, but an unexpected error appears at the end, which makes it impossible to install it
download the MATLAB installer again and reinstall it. Note that you don’t need to reinstall it all. Just select the toolbox you want

After matlab2018a is successfully installed, a licensing error appears when it is opened: – 8523

Article catalog

1. Problem description 2. Problem solving

1. Problem description

After matlab 2018a is successfully installed, a licensing error appears when it is opened: – 8523:

2. Problem solving

Delete the shortcut of MATLAB automatically created on the desktop, find .../bin/win64/matlab.exe , and then right-click 'to run' as an administrator, otherwise an error will be reported. Right click this file and send the shortcut to the desktop, so that the desktop can open MATLAB.

Matlab 2018a cracked the licensing error: – 8523

Matlab 2018a cracked the licensing error: – 8523

The online cracking method is described as follows: after installation, the license_ Copy standalone.lic to the license folder of MATLAB folder; Then copy netapi32.dll to bin \ win64 folder of MATLAB folder and overwrite it.

After this operation, the program will report 8523 error, and some people on the Internet say the method is OK, others say no, but they can’t find a fundamental solution. I installed it under win10 and reported the same error. After the personal test, the following methods are effective:

1. Run bin \ win64 \ activate_ Matlab.exe, select license_ Standard.lic file registration (this step may be omitted)

2. Do not open the program from the desktop shortcut. Run bin \ matlab.exe in the installation directory to open it. If the problem is solved, you can also resend this file and overwrite it with the desktop shortcut. The original file path is OK, but I haven’t studied why not.