Tag Archives: Deep learning

Vscode Tensorboard Error: We failed to start a TensorBoard session due to the following error: Command fa

When vscode opens the tensorboard, an error is reported:We failed to start a TensorBoard session due to the following error: Command failed: conda activate python && echo ‘e8b39361-0157-4923-80e1-22d70d46dee6’ && python /home/zhangyulan/.vscode-server/extensions/ms-python.python-2022.14.0/pythonFiles/printEnvVariables. py CommandNotFoundError: Your shell has not been properly configured to use ‘conda activate’. To initialize your shell, run $ conda init < SHELL_NAME> Currently supported shells are: – bash – fish – tcsh – xonsh – zsh – powershell See ‘conda init –help’ for more information and options. IMPORTANT: You may need to close and restart your shell after running ‘conda init’.

The main reason for the above problems is the version update.

Solution:

1. Make sure that in the .vscode-server/bin directory, delete the lock file xxxx-lock xxx, or not if it is not there. The file is shown in the following figure.

2. Return the python and balance extensions of vscode to 2022.14.0 and 2022.9.10, respectively, which are the versions one month ago. But I can’t go back to the version one month ago, just go back to the version one year ago

[Solved] PyTorch Error: TypeError: exceptions must derive from BaseException

Project scenario:

PyTorch reports an error: TypeError: exceptions must deliver from BaseException

Problem description

In base_options.py, set the –netG parameters to be selected only from these.

self.parser.add_argument('--netG', type=str, default='p2hed', choices=['p2hed', 'refineD', 'p2hed_att'], help='selects model to use for netG')

However, when selecting netG, the code is written as follows:

def define_G(input_nc, output_nc, ngf, netG, n_downsample_global=3, n_blocks_global=9, n_local_enhancers=1, 
             n_blocks_local=3, norm='instance', gpu_ids=[]):    
    norm_layer = get_norm_layer(norm_type=norm)     
    if netG == 'p2hed':    
        netG = DDNet_p2hED(input_nc, output_nc, ngf, n_downsample_global, n_blocks_global, norm_layer)
    elif netG == 'refineDepth':
        netG = DDNet_RefineDepth(input_nc, output_nc, ngf, n_downsample_global, n_blocks_global, n_local_enhancers, n_blocks_local, norm_layer)
    elif netG == 'p2h_noatt':        
        netG = DDNet_p2hed_noatt(input_nc, output_nc, ngf, n_downsample_global, n_blocks_global, n_local_enhancers, n_blocks_local, norm_layer)
    else:
        raise('generator not implemented!')
    #print(netG)
    if len(gpu_ids) > 0:
        assert(torch.cuda.is_available())   
        netG.cuda(gpu_ids[0])
    netG.apply(weights_init)
    return netG

Cause analysis:

Note that there is no option of ‘rfineD’, so when running the code, the program cannot find the network that netG should select, so it reports an error.

Solution:

In fact, change the “elif netG==’refineDepth’:”  to “elif netG==’refineD’:”. it will be OK!

torchvision.dataset Failed to Download CIFAR10 Error [How to Solve]

An error occurred while using dataset to download the dataset

urllib.error.URLError:urlopen error unknown url type:https

Considering that there is no import ssl, add the following command

**import ssl
ssl._create_default_https_context = ssl._create_unverified_context**

Run again to import ssl

import ssl report an error: DLL load fail error

Solution:

First, configure the environment variable, find the current python installation directory, and add the following three paths to the PATH of the system variable

**E:\Anaconda3\envs\pytorch;      #python.exe所在路径
  E:\Anaconda3\envs\pytorch\Scripts;		
  E:\Anaconda3\envs\pytorch\Library\bin**

Then find the files libcrypto-1_1.dll and libssl-1_1.dll in the bin folder and copy them to the DLLs path.

This solves the download problem

[Solved] PyTorch Lightning Error: KeyError: ‘hidden_states‘

How to Solve PyTorch Lightning error KeyError: ‘hidden_ states’

Problem description: PyTorch Lightning error: KeyError: ‘hidden_ states’.

model = BertModel.from_pretrained('bert-base-uncased')

Solution: add a parameter after the above code, config=BertConfig.from_pretrained(‘bert-base-uncased’,output_hidden_states=True), as below:

model = BertModel.from_pretrained('bert-base-uncased', config=BertConfig.from_pretrained('bert-base-uncased',output_hidden_states=True))

[Solved] RuntimeError: NCCL error in: XXX, unhandled system error, NCCL version 2.7.8

Project scenario:

This problem is encountered in distributed training,

Problem description

Perhaps parallel operation is not started???（

Solution:

(1) First, check the server GPU related information. Enter the pytorch terminal to enter the code

python
torch.cuda.is_available()# to see if cuda is available.
torch.cuda.device_count()# to see the number of gpu's.
torch.cuda.get_device_name(0)# to see the gpu name, the device index starts from 0 by default.
torch.cuda.current_device()# return the current device index.

Ctrl+Z Exit
(2) cd enters the upper folder of the file to be run

 CUDA_VISIBLE_DEVICES=0,1,2,3,4,5 python -m torch.distributed.launch --nproc_per_node=6 #启动并行运算

Plus files to run and related configurations

 CUDA_VISIBLE_DEVICES=0,1,2,3,4,5 python -m torch.distributed.launch --nproc_per_node=6  src_nq/create_examples.py --vocab_file ./bert-base-uncased-vocab.txt \--input_pattern "./natural_questions/v1.0/train/nq-train-*.jsonl.gz" \--output_dir ./natural_questions/nq_0.03/\--do_lower_case \--num_threads 24 --include_unknowns 0.03 --max_seq_length 512 --doc_stride 128

Problem-solving!

[Solved] RuntimeError: Error(s) in loading state dict for YOLOX:

After training the model, an error occurs when running the demo.py inference file in YOLOX, and the running code with the error is as follows:

Run Code

python tools/demo.py image -f exps/example/yolox_voc/yolox_voc_s.py -c YOLO_outputs/yolox_voc_s_1/best_ckpt.pth  --path assets/dog.jpg --conf 0.25 --nms 0.45 --tsize 640 --save_result --device [cpu/gpu]

Note:

 -f exps/example/yolox_voc/yolox_voc_s.py

This command must match, not the yolox used for testing before training_s.py, which is configured by yourself. If you don’t correct it, you will always report the following errors.

Of course, if the above instructions are OK, this error still occurs, that is, the category corresponding error in the demo.

Take my own example, I use VOC format datasets, but the default in the demo file is COCO_CLASSES, so this will definitely report an error, so we have to change it in the demo.py file.

First, find the file yolox/data/datasets/_init_.py and add the following code to the file.

from .voc_classes import VOC_CLASSES

Then enter tools/demo.py file

About 15 lines, Modify

from yolox.data.datasets import COCO_CLASSES

to

from yolox.data.datasets import VOC_CLASSES

Modify about 100 lines of cls_names in Predictor:

to

Set the function of about 300 lines

Change to

No error will be reported during operation, successful! NICE!

[Solved] Pytorch Error: RuntimeError: expected scalar type Double but found Float

Problem description:

This error occurs when LSTM is used for data training, I convert the numpy data directly to the tensor data type in the torch：

RuntimeError: expected scalar type Double but found Float

Cause analysis:

The data type of the tensor is incorrect

x_train_tensor = torch.from_numpy(x_train)
y_train_tensor = torch.from_numpy(y_train)

Solution:

Convert the original tensor to the torch.float32 type

x_train_tensor = torch.from_numpy(x_train).to(torch.float32)
y_train_tensor = torch.from_numpy(y_train).to(torch.float32)

[Solved] AttributeError: module ‘distutils‘ has no attribute ‘version‘

mmyolo + tensorboard failed to start error:

File "D:\Anaconda3\envs\mmyo\lib\site-packages\mmengine\visualization\vis_backend.py", line 495, in _init_env
    from torch.utils.tensorboard import SummaryWriter
  File "D:\Anaconda3\envs\mmyo\lib\site-packages\torch\utils\tensorboard\__init__.py", line 4, in <module>
    LooseVersion = distutils.version.LooseVersion
AttributeError: module 'distutils' has no attribute 'version'

Reason:

The version of setuptools is too higher.

Solution:
Install the lower version of setuptools via the following command:
 

pip install setuptools==56.1.0

[Solved] AttributeError: ‘HTMLWriter‘ object has no attribute ‘_temp_names‘

Error Message (Error 1):

TypeError: render() got an unexpected keyword argument ‘mode‘

Solution for Error1:

Tried setting gym and pyglet to

  • gym:0.17.1
  • pyglet:1.5.0

Note: This method will solve the problem above.

However, An new error (Error 2) will be reported:

AttributeError: ‘HTMLWriter’ object has no attribute ‘_temp_names’

Solution for Error2:

  • Open the .py file where you wrote your code (the same file you wrote your code in)
  • Find your animate_frames method. (If you don’t have it, you can ignore it, I don’t have it, then just put the first block of code from step 3 at the top)
  • Add the code before the animate_frames method (add the package to the top).
import matplotlib.pyplot as plt
from IPython.display import HTML

def display_animation(anim):
    plt.close(anim._fig)
    return HTML(anim.to_jshtml())

Find the following code:

display(display_animation(anim, default_mode='XXX'))

Change it to:

display(display_animation(anim))

The following code can be deleted or ignored:

from JSAnimation.IPython_display import display_animation

[Solved] ONNXImporter::handleNode DNN/ONNX和create layer “onnx::Gather_384“ of type “NonMaxSuppression“

Leave a reply

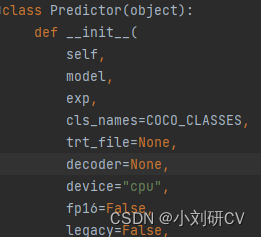
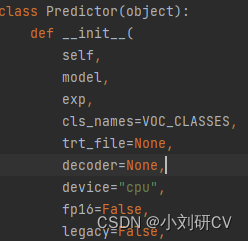
Today I encountered a lot of OpenCV loading model errors when debugging the yolov7 model conversion and loading problemm There is no way to fully display it due to the title length limit, I will post it here in its entirety.

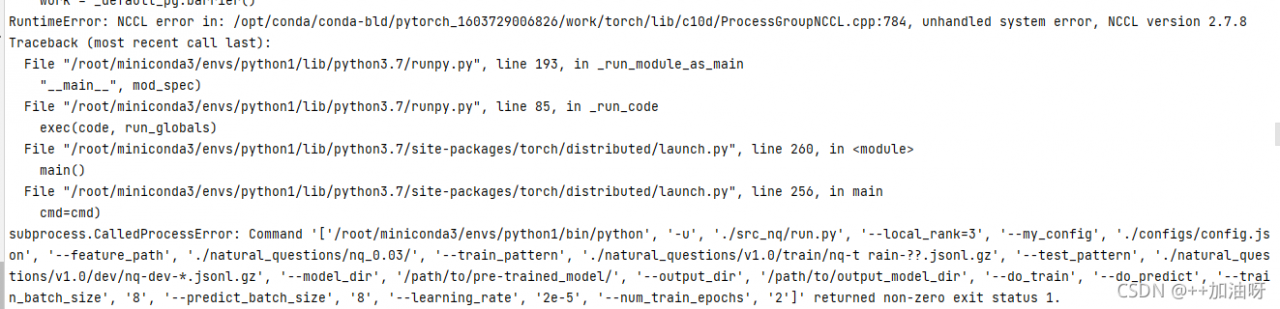
[ERROR:0] global D:\opencv-python\opencv\modules\dnn\src\onnx\onnx_importer.cpp (720) cv::dnn::dnn4_v20211004: :ONNXImporter::handleNode DNN/ONNX: ERROR during processing node with 5 inputs and 1 outputs: [NonMaxSuppression]:(onnx::Gather_384)
cv2.error: OpenCV(4.5.4) D:\opencv-python\opencv\modules\dnn\src\onnx\onnx_importer.cpp:739: error: (- 2:Unspecified error) in function 'cv::dnn::dnn4_v20211004::ONNXImporter::handleNode'
cv2.error: OpenCV(4.5.4) D:\opencv-python\opencv\modules\dnn\src\onnx\onnx_importer.cpp:739: error: (- 2:Unspecified error) in function 'cv::dnn::dnn4_v20211004::ONNXImporter::handleNode'
> Node [NonMaxSuppression]:(onnx::Gather_384) parse error: OpenCV(4.5.4) D:\opencv-python\opencv\modules\dnn\src\dnn.cpp:615: error: (-2:Unspecified error) Can't create layer "onnx::Gather_384" of type "NonMaxSuppression" in function 'cv::dnn::dnn4_v20211004::LayerData::getLayerInstance&# 39;

At this time, I think of a way to compare my own model with the official model one by one,Comparison of one node and one node, Finally found the problem at the end.

[Official Model]

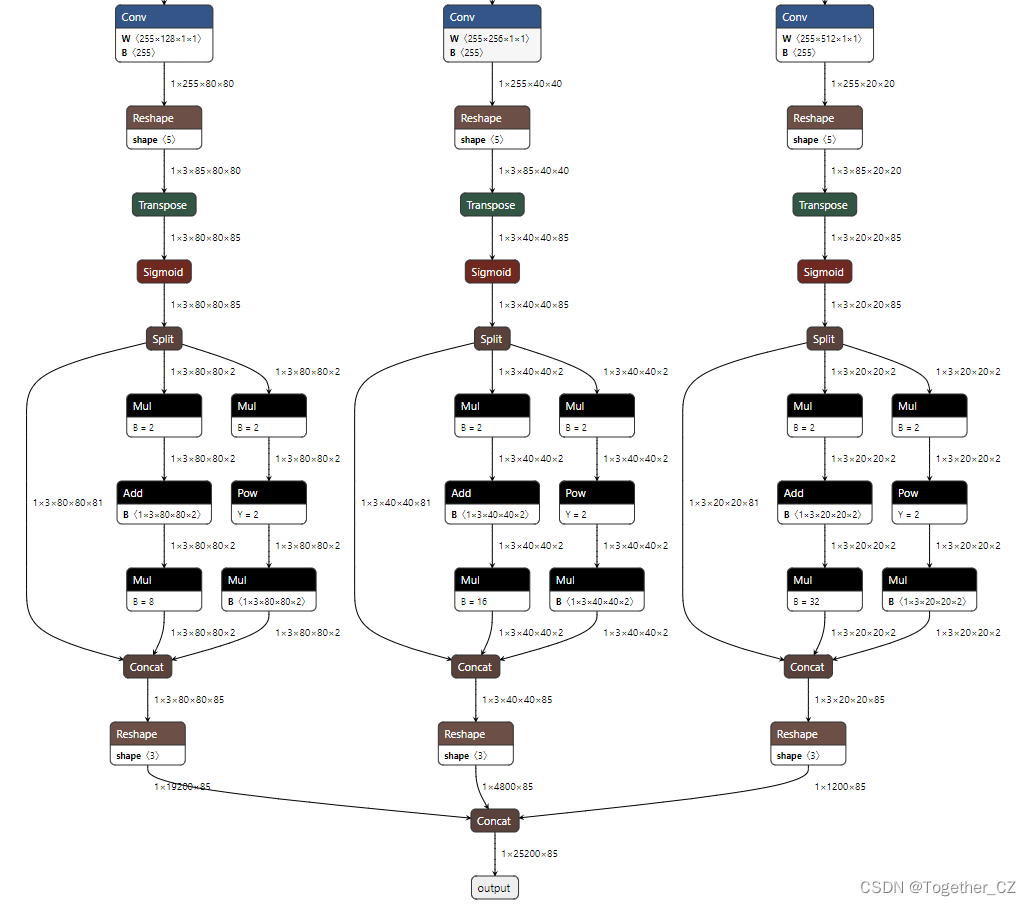
[My own model]

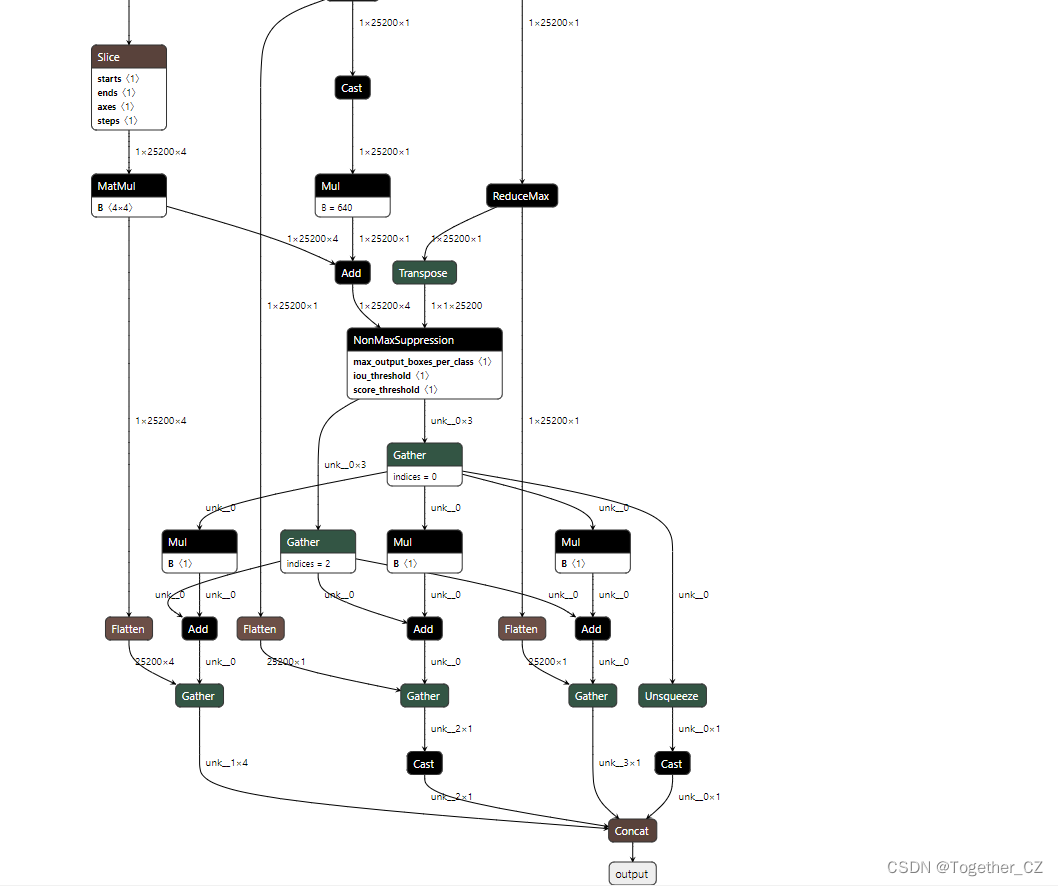
Seeing this, I’m wondering if there is such a big difference?？It shouldn’t be，It’s all models built from the same code，So I started to trace the source，Sure enough Problem found.

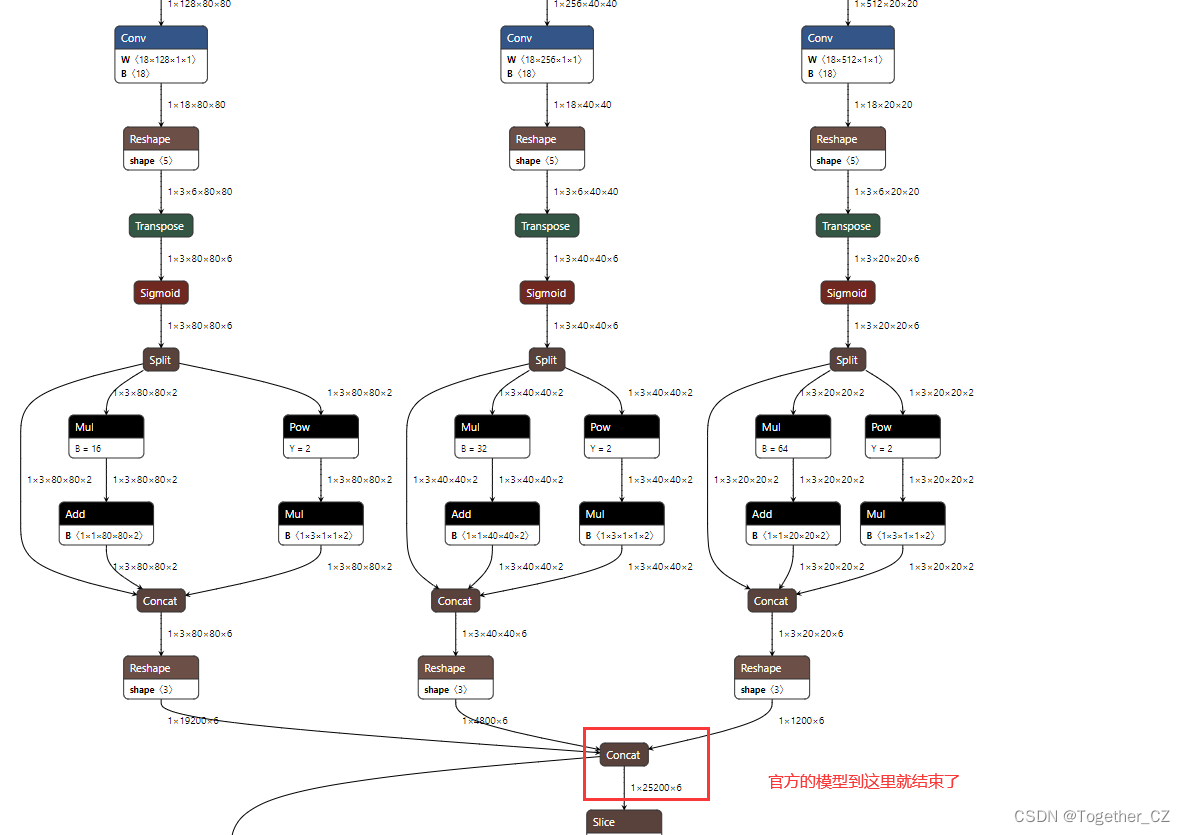
At the position of my red frame, the official model ends here, and there is a large string of, tensor shapes for debugging both by printing, I guess that there may be a problem with the parameter settings during the model export process, So I tried to verify basically all the uncertain parameters, I found the problem.

In order to facilitate your understanding, I am giving my original conversion operation command here：

python export.py --weights best.pt --grid --end2end --simplify --topk-all 100 --iou-thres 0.65 --conf-thres 0.35 --img-size 640 640 --max-wh 640

This is the command after：

python38 export.py --weights best.pt --grid --simplify --topk-all 100 --iou-thres 0.65 --conf-thres 0.35 --img -size 640 640 --max-wh 640

See the difference, In fact, it is caused by the parameter end2end, After the modification, my model is as follows：

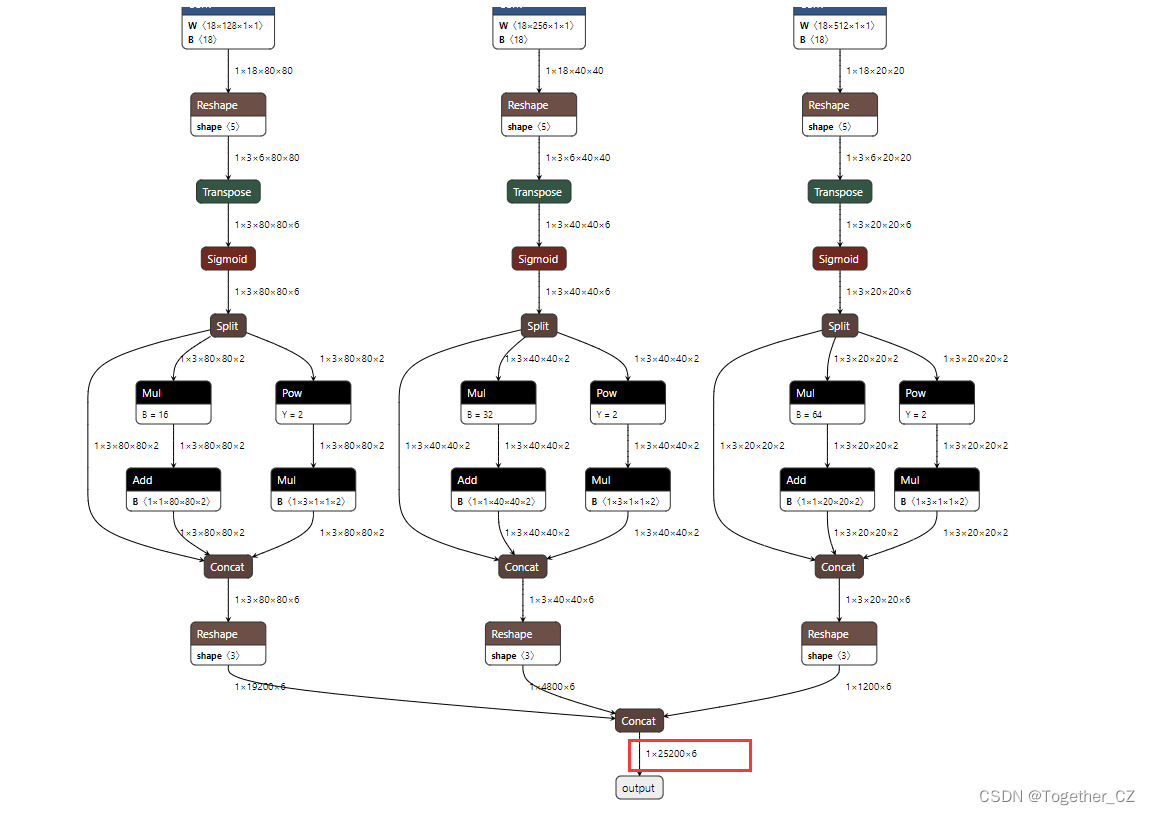
Because what I am doing here is the detection of the category, so the final output is: 1x25200x6, and the official one is: 1x25200x85.

onnx error: ImportError: /home/dy/anaconda3/envs/torch/lib/python3.6/site-packages/onnx…

Leave a reply

onnx error:


import onnx



Traceback (most recent call last):
  File "torch2onnx.py", line 3, in 
    import onnx
  File "/home/dy/anaconda3/envs/torch/lib/python3.6/site-packages/onnx/__init__.py", line 5, in 
    from .onnx_cpp2py_export import ONNX_ML
ImportError: /home/dy/anaconda3/envs/torch/lib/python3.6/site-packages/onnx/onnx_cpp2py_export.cpython-36m-x86_64-linux-gnu.so: undefined symbol: _ZN6google8protobuf7Message17CopyWithSizeCheckEPS1_RKS1_

Solution:

git clone https://github.com/onnx/onnx.git

cd onnx

git submodule update –init –recursive

# Optional: prefer lite proto

export CMAKE_ARGS=”-DONNX_USE_PROTOBUF_SHARED_LIBS=ON”

export CMAKE_ARGS=-DONNX_USE_LITE_PROTO=ON

pip install -e .

[Solved] RuntimeError: CUDA error: CUBLAS_STATUS_EXECUTION_FAILED when calling `cublasSgemm

Problem

After training to a certain number of iterations, an error is reported:
RuntimeError: CUDA error: CUBLAS_STATUS_EXECUTION_FAILED when calling cublasSgemm( handle, opa, opb, m, n, k, &alpha, a, lda, b, ldb, &beta, c, ldc)

Possible causes

  • The shape dimension does not match
  • Variables are not on the same device
  • pytorch and cuda versions do not match

Solution

Add os.environ['CUDA_VISIBLE_DEVICES'] = '0' at the beginning of the train.py file, and set device='cuda'.
But there is a strange phenomenon: if you do not set the visible gpu, but specify device='cuda:0', it will also report an error.