The concept of     deformable convolution was proposed in the paper: deformable convolutional networks
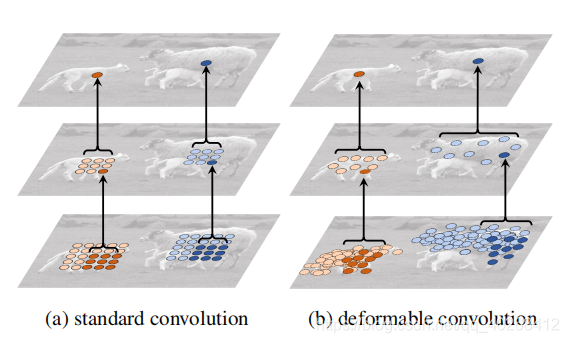
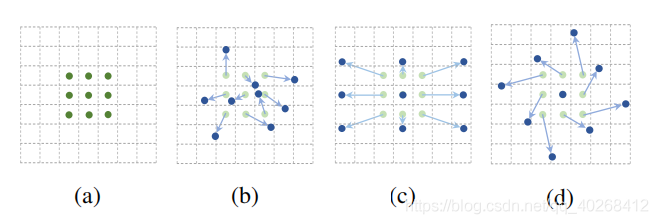
in this paper    as the name suggests, deformable convolution is derived from the concept of standard convolution. In standard convolution operation, the convolution core’s action area is always in the rectangular area of the size of the standard convolution core around the center point (as shown in figure a below), while deformable convolution can be an irregular area (as shown in Figure B, C, D below, where the offset of B is random; C, D are special cases).

The implementation method of     deformation convolution is shown in the following figure:

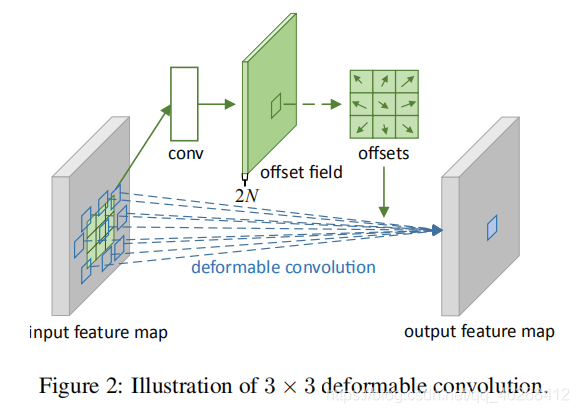
The dimension information of each part is as follows:
     input feature map: (batch, h, W, c)
    output feature map: (batch, h, W, n)
    offset field: (batch, h, W, 2n)
     offset field is obtained by standard convolution operation on the original graph, and the number of channels is 2n, which means n 2-dimensional offsets

（

△

x

，

△

y

）

（△x，△y）

(△ x, △ y), n is the number of convolution kernels, that is, the number of channels of output characteristic layer. The process of deformation convolution can be described as follows: firstly, standard convolution is performed on the input feature map to obtain n 2-dimensional offsets

（

△

x

，

△

y

）

（△x，△y）

(△ x, △ y), and then modify the values of each point on the input feature map (let feature map be

P

P

P. Namely

P

（

x

，

y

）

=

P

（

x

+

△

x

，

y

+

△

y

）

P（x，y）=P（x+△x，y+△y）

P (x, y) = P (x + △ x, y + △ y), when

x

+

△

x

x+△x

When x + △ x is a fraction, bilinear interpolation is used

P

（

x

+

△

x

，

y

+

△

y

）

P（x+△x，y+△y）

P（x+△x，y+△y））。 Form n feature maps, and then use n convolution kernels to convolute one by one to get the output.
The calculation results of   standard convolution and deformation convolution are shown in the following figure: