recall that in the previous section, we introduced the house-price based modeling under a single variable, the cost function, and the design of the gradient descent method. In this section, we extended the problem to the generalization, and how to deduce the gradient descent process under the change of a single variable into a multiple variable.

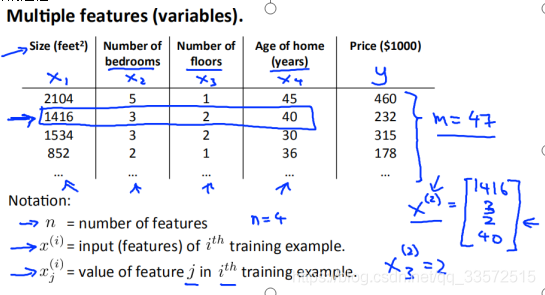
As shown in the figure, the input features are (x1,x2,x3,x4)

The output feature of

is y

The total number of samples

is m

It’s

and we’re assuming that the fitting function is

, then we want to minimize the cost function, the solution of the parameter is shown in the figure

in order to understand the cost function when there are only two variables, the cost function is shown in the figure

X1 = size (0-2000)

X2 = bedroom (0-5)

by observing the left figure, we find that when x1 and x2 are greatly different, the cost function image is of thin and tall shape. In this case, the route of gradient descent to the optimal solution is more tortuous, that is, the regression is more difficult. When the parameters are relatively close, as shown in the right figure, the gradient descent route is closer to a linear line, that is, the gradient descent is easier.

so we need to scale the feature

scale to [0-1] feature/ the total of number

method 2 scales to [-1, 1] (feature – mean)/the total of number

, of course, as shown in the figure, if the parameters are not far apart, such as between [-3, 3], there is no need to scale the feature

in the previous section, we talked about the effect of a on regression in the case of gradient descent, and then we specifically discuss the value of a

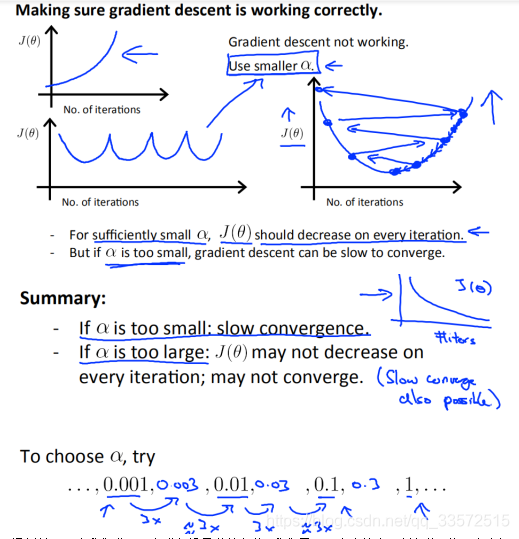
through the previous observation, we found that in order to find the parameters of the hypothesis function, we need to update the parameters step by step, and then introduce another solution method (through mathematical reasoning method: normal equation, one step in place to find the optimal parameter)

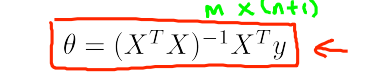
let’s look at this formula, X is a row vector, (XTX) is an n by n matrix, and solving its inverse requires order n3 complexity, so we don’t use this method when we have more features.