Given a binary tree, check whether it is balanced or not.
Analyze:
Consider a height-balancing scheme where following conditions should be checked to determine if a binary tree is balanced.
An empty tree is height-balanced. A non-empty binary tree T is balanced if:
1) Left subtree of T is balanced
2) Right subtree of T is balanced
3) The difference between heights of left subtree and right subtree is not more than 1.
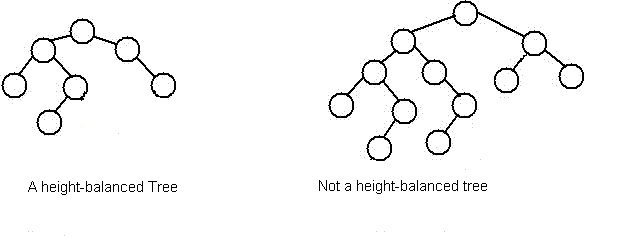
The above height-balancing scheme is used in AVL trees. The diagram below shows two trees, one of them is height-balanced and other is not. The second tree is not height-balanced because height of left subtree is 2 more than height of right subtree.
To check if a tree is height-balanced, get the height of left and right subtrees. Return true if difference between heights is not more than 1 and left and right subtrees are balanced, otherwise return false.
Code:
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
if (Math.abs(height(root.left) - height(root.right)) > 1) return false;
return isBalanced(root.left) && isBalanced(root.right);
}
public int height(TreeNode root) {
if (root == null) return 0;
return Math.max(height(root.left), height(root.right)) + 1;
}
}The complexity of the code above is O(N^2). However, some interviewers may ask to provide solution with O(N) complexity. Below is the solution with O(N) complexity. The main idea is if the subtree is balanced, return the true height, else, return -1. Therefore, the parent node of that unbalanced subtree also has -1 height.
public class Solution {
public boolean isBalanced(TreeNode root) {
return getDepth(root) >= 0;
}
public int getDepth(TreeNode node) {
if (node == null) return 0;
int leftDepth = getDepth(node.left);
if (leftDepth < 0) return -1;
int rightDepth = getDepth(node.right);
if (rightDepth < 0) return -1;
if (Math.abs(leftDepth - rightDepth) > 1) return -1;
return Math.max(leftDepth, rightDepth) + 1;
}
}Reference:
http://www.geeksforgeeks.org/how-to-determine-if-a-binary-tree-is-balanced/
http://blog.theliuy.com/2012/balanced-binary-tree/