Binary tree is a very important data structure, many other data structures are based on the evolution of binary tree. For binary tree, there are depth traversal and breadth traversal. Depth traversal has three traversal methods: preorder, middle order and postorder. Breadth traversal is what we usually call level traversal. Because the definition of tree itself is a recursive definition, it is not only easy to understand but also very concise to use the recursive method to realize the three traversal of tree. For breadth traversal, it needs the support of other data structures, such as heap. Therefore, for a piece of code, readability is sometimes more important than the efficiency of the code itself.
The four main traversal ideas are as follows
Preorder traversal: root node — & gt; left subtree — & gt; right subtree
Middle order traversal: left subtree — & gt; root node — & gt; right subtree
Postorder traversal: left subtree — & gt; right subtree — & gt; root node
Level traversal: just traverse by level
For example, find the following binary tree traversal
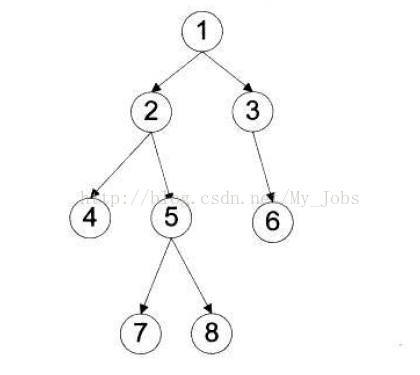
Preorder traversal: 1.2.4.5.7.8.3.6
Middle order traversal: 4 ﹣ 2 ﹣ 7 ﹣ 5 ﹣ 8 ﹣ 1 ﹣ 3 ﹣ 6
Postorder traversal: 4 ﹣ 7 ﹣ 8 ﹣ 5 ﹣ 2 ﹣ 6 ﹣ 3 ﹣ 1
Level traversal: 1 ﹣ 2 ﹣ 3 ﹣ 4 ﹣ 5 ﹣ 6 ﹣ 7 ﹣ 8
1、 Preorder traversal
1) According to the traversal idea mentioned above: root node — & gt; left subtree — & gt; right subtree, it is easy to write recursive version:
public void preOrderTraverse1(TreeNode root) {
if (root != null) {
System.out.print(root.val+" ");
preOrderTraverse1(root.left);
preOrderTraverse1(root.right);
}
}2) Now let’s talk about the non recursive version:
According to the order of preorder traversal, first visit the root node, then visit the left and right subtree. Therefore, for any node, the first part is to access it directly, and then repeat the above steps when judging whether the left subtree is empty or not until it is empty. If it is empty, you need to access the right subtree. Note that after accessing the left child, you need to access the right child in turn. Therefore, you need the support of stack as a data structure. For any node, the specific steps are as follows:
a) Access it, and put the node into the stack, and set the current node as the left child;
b) Judge whether the node node is empty. If it is empty, take out the top node of the stack and leave the stack, and set the right child as the current node; otherwise, repeat step a) until the current node is empty or the stack is empty (it can be found that the nodes in the stack are stored just to access the right child)
The code is as follows:
public void preOrderTraverse2(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
TreeNode pNode = root;
while (pNode != null || !stack.isEmpty()) {
if (pNode != null) {
System.out.print(pNode.val+" ");
stack.push(pNode);
pNode = pNode.left;
} else { //pNode == null && !stack.isEmpty()
TreeNode node = stack.pop();
pNode = node.right;
}
}
}2、 Middle order traversal
1) According to the above traversal idea: left subtree — & gt; root node — & gt; right subtree, it is easy to write recursive version:
public void inOrderTraverse1(TreeNode root) {
if (root != null) {
inOrderTraverse1(root.left);
System.out.print(root.val+" ");
inOrderTraverse1(root.right);
}
}2) non recursive implementation, with the explanation of the preceding order, the middle order is relatively simple, the same reason. It’s just that the order of access is moved to the time of stack exit. The code is as follows:
public void inOrderTraverse2(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
TreeNode pNode = root;
while (pNode != null || !stack.isEmpty()) {
if (pNode != null) {
stack.push(pNode);
pNode = pNode.left;
} else { //pNode == null && !stack.isEmpty()
TreeNode node = stack.pop();
System.out.print(node.val+" ");
pNode = node.right;
}
}
}3、 Postorder traversal
1) According to the traversal idea mentioned above: left subtree — & gt; right subtree — & gt; root node, it is easy to write recursive version:
public void postOrderTraverse1(TreeNode root) {
if (root != null) {
postOrderTraverse1(root.left);
postOrderTraverse1(root.right);
System.out.print(root.val+" ");
}
}2) Non recursive code, not to write
4、 Level traversal
Hierarchy traversal code is relatively simple, just need a queue, first add the root node in the queue. Then, for any node, when it is out of the queue, it can be accessed. At the same time, if the left child and the right child are not empty, enter the queue. The code is as follows:
public void levelTraverse(TreeNode root) {
if (root == null) {
return;
}
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.print(node.val+" ");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}5、 Depth first traversal
In fact, depth traversal is the pre order, middle order and post order above. But in order to ensure that it corresponds to breadth first traversal, it is also written here. The code is also easy to understand. In fact, it is preorder traversal. The code is as follows:
0
public void depthOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
LinkedList<TreeNode> stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
System.out.print(node.val+" ");
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}Finally finished!