- Overflow ConditionBinary ArithmeticAdding Unsigned NumbersOverflow Detection Circuit for Unsigned AdditionAdding Signed NumbersThe Full Adder Truth TableAdding the Sign BitsThe Overfow OutputSigned Numbers AdditionSigned Numbers Addition, Cont.Signed Numbers Addition, Cont.Signed Numbers Addition, Cont.Signed Numbers Addition, Cont.Overflow Detection Circuit for 2’s Complement AdditionMisconceptions about Overflow
1. Overflow Condition
Arithmetic operations have a potential to run into a condition known as overflow. Overflow occurs with respect to the size of the data type that must accommodate the result. Overflow indicates that the result was too large or too small to fit in the original data type. When two signed 2’s complement numbers are added, overflow is detected if:
- both operands are positive and the result is negative, or both operands are negative and the result is positive.
When two unsigned numbers are added, overflow occurrs if
there is a carry out of the leftmost bit.
2. Binary Arithmetic
Computers don’t know the difference between signed and unsigned binary numbers. This is a good thing, because it makes logic circuits fast. This is also a bad thing, because distinguishing between signed and unsigned is our responsibility. The distinction is very important when detecting an overflow after addition or subtraction. Correct approach to detect the overflow is to consider two separate cases:
- Overflow when adding unsigned numbers.
- Overflow when adding signed numbers.
3. Adding Unsigned Numbers
- Let’s first solve the problem for addition of one-bit quntities:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
The last line indicates that we have a carry output. That is, one-bit quantity cannot accommodate (1 + 1). Therefore, larger data type is required for (1 + 1) to succeed. When multi-bit unsigned quantities are added, overflow occurrs if there is a carry out from the leftmost (most significant) bit.
4. Overflow Detection Circuit for Unsigned Addition
Overflow detection circuit for unsigned binary addition: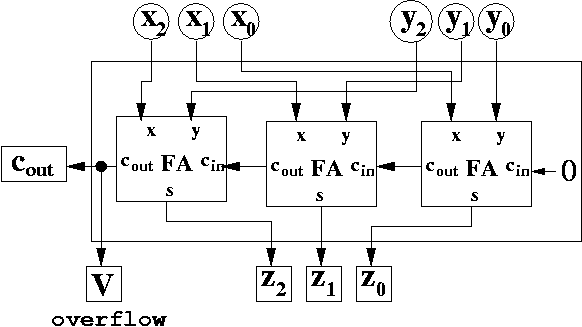 
5. Adding Signed Numbers
Consider overflow detection when adding two one-bit signed quntities. Although one bit is required to represent the data, another bit has to represent the sign. Therefore, two-bit data type is required:
|
Recall that to represent 2’s complement negative number, we must
|
6. The Full Adder Truth Table
Recall the truth table for the 2’s complement full adder logic:
|
The truth table includes five columns with three inputs and two outputs.
|
7. Adding the Sign Bits
|
The full adder knows nothing about the difference between signed and unsigned numbers. In 2’s complement binary representation, the sign bit is simply the leftmost, or most significant, bit of the data type. The full adder circuit will be adding the sign bit column just as any other bit. |
8. The Overfow Output
|
Full adder truth table for the sign bit can be extended to include new output which indicates if overfow condition has occured. Our task is to populate the OVERFLOW column with corresponding values. |
9. Signed Numbers Addition
Two-bit signed data type:
|
Notice that when operands have opposite signs, their sum will never overflow:
1 + -2 = -1
1 + -1 = 0
Therefore, overflow can only occur when the operands have the same sign: 1 + 1 = 2
-2 + -2 = -4
-2 + -1 = -3
None of the results { 2, -4, -3 } can fit into the two-bit signed data type. |
10. Signed Numbers Addition, Cont.
|
When operands have opposite signs, their sum will never overflow. |
11. Signed Numbers Addition, Cont.
|
There is no overflow, if: both operands are positive and the sum is positive. both operands are negative and the sum is negative. |
12. Signed Numbers Addition, Cont.
|
When two signed 2’s complement numbers are added, overflow is detected if:
|
13. Signed Numbers Addition, Cont.
|
Notice that overflow occurs only when CARRYin ≠ CARRYout or simply V = Cin XOR Cout where V is the overflow signal. |
14. Overflow Detection Circuit for 2’s Complement Addition
Overflow detection circuit for 2’s complement addition 
15. Misconceptions about Overflow
Specific overflow detection requires knowing the operation and the representation. Overflow occurs when you do some operation to two valid representations…
… and the result can not be represented in the representation because the value is too large or too smal. Overflow detection is detecting overflow for a specific representation…
… Too often people mistake overflow condition for unsigned overflow, when the carry out is 1. Overflow detection for 2’s complement addition is different:
One way to detect it is to XOR the carry in and the carry out.
Read More:
- Opencv detection yolov4 target detection video stream error
- call to member function bind_param() on boolean………..
- Solution of error in CAD license detection
- How to use matlab to solve equation
- Edge detection: two methods
- Failed startup of context o.e.j.w WebAppContext@532aaf8a {/admin,file:/D:/Develop/activeM
- The C language qsort() function reports an error for overflow of – 2147483648 and 2147483648
- Oci-22053: overflow error problem
- Arithmetic overflow error converting identity to data type int
- Convex hull detection and convex hull vertex solution of PCL point cloud Library
- How to Solve Int Data overflow error
- Out of memory overflow solution for idea running error
- Arithmetical overflow error converting expression to data type datetime
- OpenGL runtime returned 1283 (stack overflow) error
- Differences between Java stack overflow ror and outofmemoryerror
- How to Fix stack overflow error
- JNI ERROR global reference table overflow [How to Solve]
- The difference, cause and solution of memory overflow and memory leak
- Solution pandas.errors.ParserError : Error tokenizing data. C error: Buffer overflow caught
- Arithmetic overflow error converting numeric to data type numeric.