One dimensional convolution is usually used to process text, so the input is usually a long piece of text, which is a list of words
The function is defined as follows:
tf.layers.conv1d(
inputs,
filters,
kernel_size,
strides=1,
padding='valid',
data_format='channels_last',
dilation_rate=1,
activation=None,
use_bias=True,
kernel_initializer=None,
bias_initializer=tf.zeros_initializer(),
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
bias_constraint=None,
trainable=True,
name=None,
reuse=None
)The more important parameters are inputs, filters and kernel_ Size, which are described below
Inputs: input tensor. Dimension (none, a, b) is a three-dimensional tensor
None: usually the number of samples to be filled, batch_ size
A: the number of words or words in a sentence
B: vector dimension of word or word
Filters: the number of filters
kernel_ Size: the size of convolution kernel. Convolution kernel should be two-dimensional. Only one dimension needs to be specified here, because the second dimension of convolution kernel is consistent with the input word vector dimension, because for sentences, convolution can only move along the word direction, that is, it can only move in the column dimension
An example:
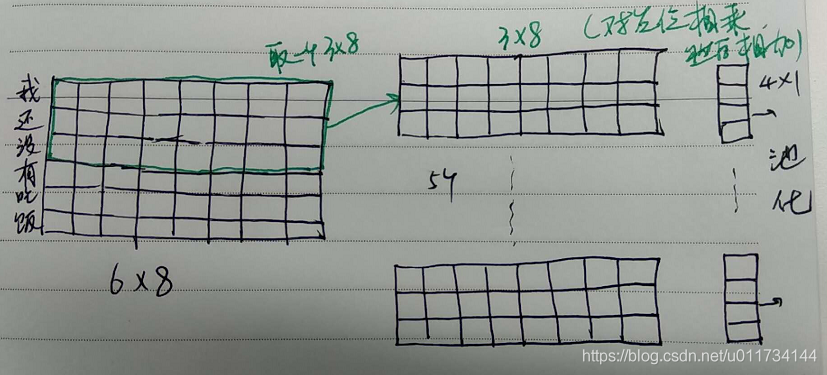
inputs = tf.placeholder (‘float’, shape=[None, 6, 8])
out = tf.layers.conv1d (inputs, 5, 3)
Note: for a sample, the sentence length is 6 words, and the dimension of the word vector is 8
filters=5, kernel_ Size = 3, so the dimension of convolution kernel is 3 * 8
Then the input 6 * 8 is convoluted by 3 * 8 convolution kernel to get a vector of 4 * 1 (4 = 6-3 + 1)
And because there are five filters, we get five 4 * 1 vectors
The drawing is as follows:
Read More:
- tf.contrib.layers .xavier_ Initializer function usage
- Two dimensional array and pointer to one dimensional array
- tf.one_ How to use hot ()
- In tensorflow tf.reduce_ Mean function
- The principle of deformable convolution
- Tensorflow in function tf.Print Method of outputting intermediate value
- The routine of benewake tfmini-s / tfmimi plus / tfluna / tf02 Pro / tf03 radar on Python
- tf.gradients is not supported when eager execution is enabled. Use tf.GradientTape instead.
- Analysis of compilation errors of “error conflicting types for function”
- Tensorflow tf.train.exponential_ Decay function (exponential decay method)
- C language write() function analysis: write failed bad address
- RuntimeError: Unable to find a valid cuDNN algorithm to run convolution
- VTK cultivation 26: basic operation of image_ Three dimensional image slice extraction
- Tensorflow UnknownError (see above for traceback): Failed to get convolution algorithm. This is pro
- Error debug in box2d createfixture Error:R6025 pure Virtual function call solution
- Type definition error – one of the causes of type definition errors is WM in Oracle_ Concat function usage
- RuntimeError: ‘lengths’ argument should be a 1D CPU int64 tensor, but got 1D cuda:0 Long tensor
- “Typeerror: invalid dimensions for image data” in Matplotlib drawing imshow() function
- raise RuntimeError(“tf.placeholder() is not compatible with “ RuntimeError: tf.placeholder() is not
- Create a D3D11 application process