Tag Archives: Deep learning

ModuleNotFoundError: No module named ‘tensorboardX‘

Yesterday, I was trying to run the code that I didn’t run through, so I tossed it on my own machine and virtual machine. As a result, I made a mistake in the environment variable. Here I record it. The error prompt says that I didn’t find ‘tensorboardx’. I checked the command and found that there was also ‘tensorboardx’. So I tried to run the python environment manually and found that the code was running normally, so If you find a similar error, don’t start to install the software as soon as you run, but see if you have installed the software correctly.

SystemError: new style getargs format but argument is not a tuple

SystemError: new style getargs format but argument is not a tuple

**

A very simple but BD less than a small bug

Read data using CV2. Reset() function, the original program: CV2. Reset (IMG, 28,56), the picture to (28,56) size. The error is as follows: systemerror: new style getargs format but argument is not a tuple!

Parameter non tuple case!
At the beginning, change 28,56 to [28,56], but it still can’t be changed to (28,56)
that is, reset (IMG, (28,56)).
just started to write programs in Python, and used Matlab before, so there are always such and such errors, I hope others can find the debug as soon as possible!
I wish you a quick and successful debug!

Deep learning: derivation of sigmoid function and loss function

1sigmoid function

1. Derivation from exponential function to sigmoid 2. Logarithm function and sigmoid 2. Sigmoid function 3. Neural network loss function derivation

1. Sigmoid function

Sigmoid function, i.e. S-shaped curve function, is as follows:
0

Function: F (z) = 11 + e − Z

Derivative: F ‘(z) = f (z) (1 − f (z))

The above is our common form. Although we know this form, we also know the calculation process. It’s not intuitive enough. Let’s analyze it.

1.1 from exponential function to sigmoid

First, let’s draw the basic graph of exponential function

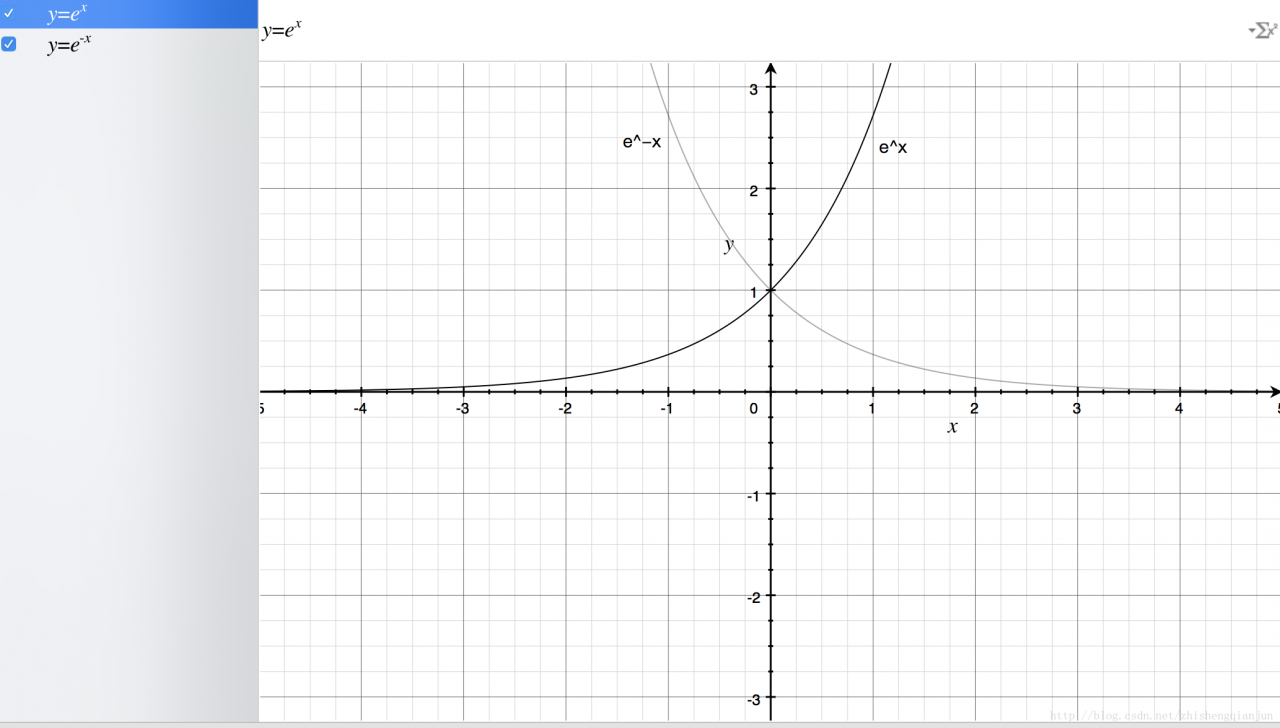
From the figure above, we get the following information: the exponential function passes (0,1) point, monotonically increasing / decreasing, and the definition field is

(−∞,+∞)

, the range is

(0,+∞)

Let’s take a look at the image of the sigmoid function

​

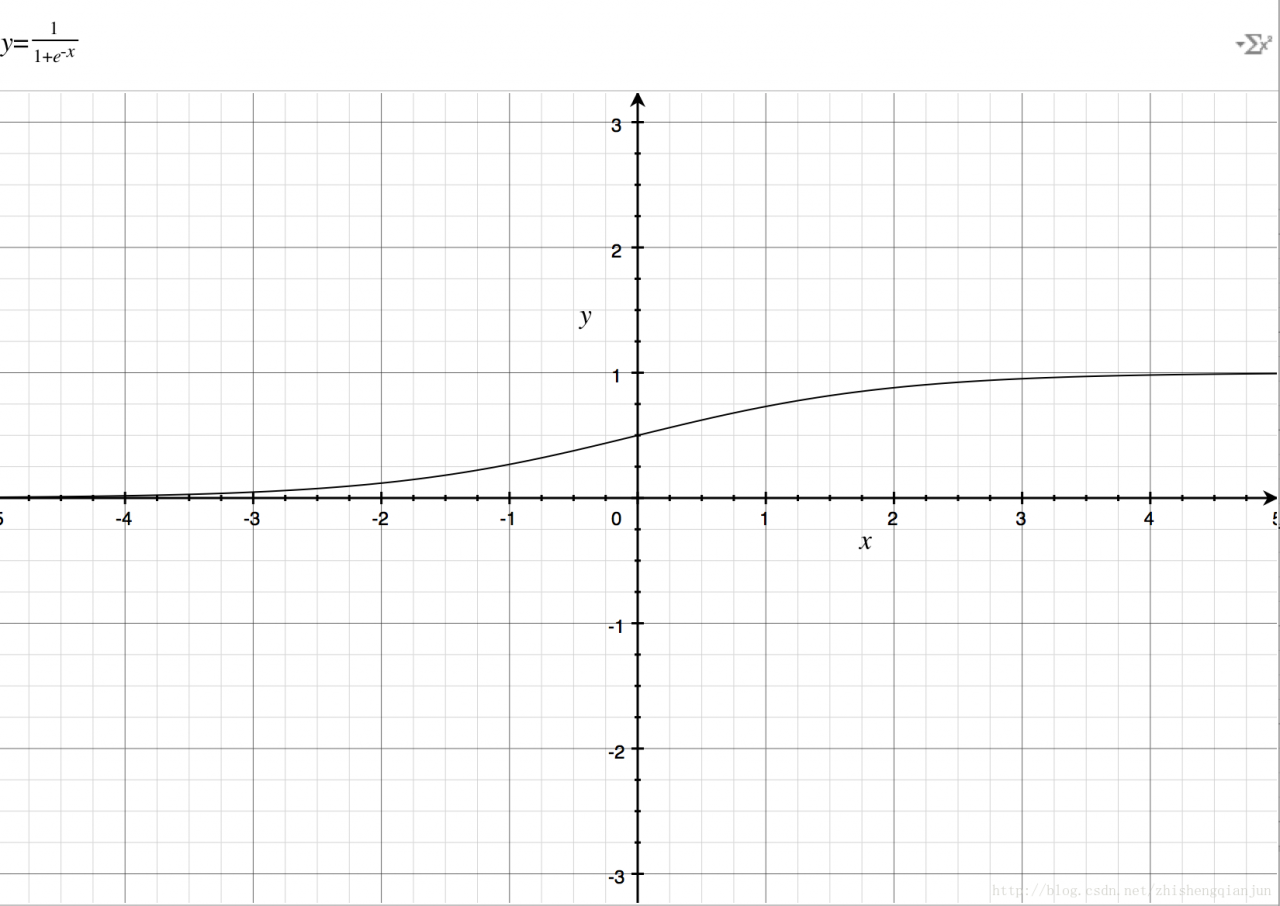
If you just

e−x

If you put it on the denominator, it’s the same as

ex

The image is the same, so add 1 to the denominator to get the image above. The domain of definition is

(−∞,+∞)

, the range is

(0,1)

Then there is a good feature, that is, no matter what

x

We can get the value between (0,1) for whatever it is;

1.2 logarithmic function and sigmoid

First, let’s look at the image of the logarithmic function

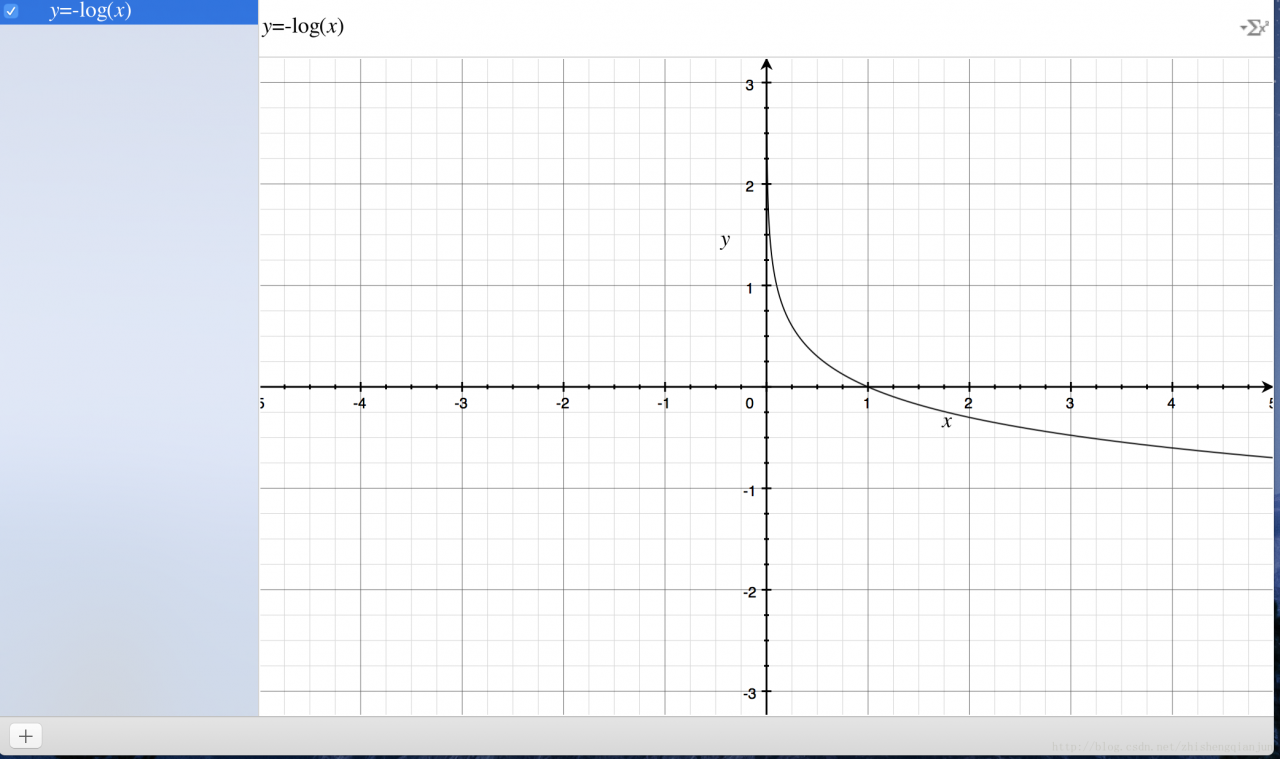
Logarithmic function of the image above, monotone decreasing, there is a better feature is in the

(0,1)

If we put the sigmoid function in front of us in the position of the independent variable, we will get the result

(0,1)

The image of the image;

How can we measure the difference between a result and the actual calculation? One idea is that if the result is closer, the difference will be smaller, otherwise, it will be larger. This function provides such an idea. If the calculated value is closer to 1, then it means that it is closer to the world result, otherwise, it is farther away. Therefore, this function can be used as the loss function of logistic regression classifier. If all the results are close to the result value, then The closer it is to 0. If the result is close to 0 after all the samples are calculated, it means that the calculated result is very close to the actual result.

2. Derivation of sigmoid function

The derivation process of sigmoid derivative is as follows:
0

f′(z)=(11+e−z)′=e−z(1+e−z)2=1+e−z−1(1+e−z)2=1(1+e−z)(1−1(1+e−z))=f(z)(1−f(z))

3. Derivation of neural network loss function

The loss function of neural network can be understood as a multi-level composite function, and the chain rule is used for derivation.

​

J(Θ)=−1m∑i=1m∑k=1K[y(i)klog((hΘ(x(i)))k)+(1−y(i)k)log(1−(hΘ(x(i)))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2

Let’s talk about the process of conventional derivation

​

e=(a+b)(b+1)

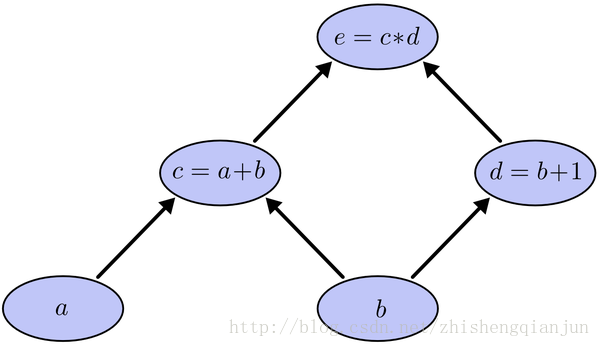
​ This is a simple composite function, as shown in the figure above. C is a function of a and E is a function of C. if we use the chain derivation rule to derive a and B respectively, then we will find out the derivative of e to C and C to a, multiply it, find out the derivative of e to C and D respectively, find out the derivative of C and D to B respectively, and then add it up, One of the problems is that in the process of solving, e calculates the derivative of C twice. If the equation is particularly complex, then the amount of calculation becomes very large. How can we only calculate the derivative once?

​

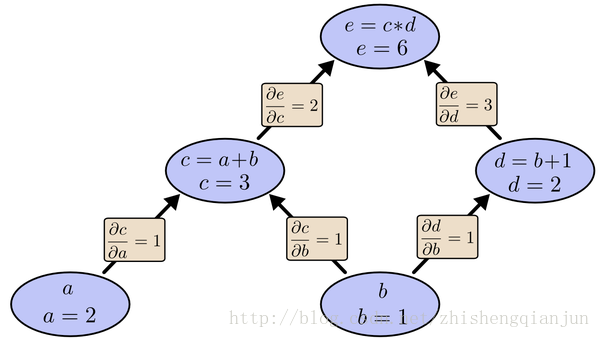
As shown in the figure above, we start from top to bottom, calculate the value of each cell, then calculate the partial derivative of each cell, and save it;

​ Next, continue to calculate the value of the sub unit, and save the partial derivatives of the sub unit; multiply all the partial derivatives of the path from the last sub unit to the root node, that is, the partial derivatives of the function to this variable. The essence of calculation is from top to bottom. When calculating, save the value and multiply it to the following unit, so that the partial derivatives of each path only need to be calculated once, from top to bottom All the partial derivatives are obtained by calculating them from top to bottom.

​ In fact, BP (back propagation algorithm) is calculated in this way. If there is a three-layer neural network with input layer, hidden layer and output layer, we can calculate the partial derivative of the weight of the loss function. It is a complex composite function. If we first calculate the partial derivative of the weight of the first layer, and then calculate the partial derivative of the weight of the second layer, we will find that there are some problems A lot of repeated calculation steps, like the example of simple function above, so, in order to avoid this kind of consumption, we use to find the partial derivative from the back to the front, find out the function value of each unit, find out the partial derivative of the corresponding unit, save it, multiply it all the time, and input the layer.

The following is a simple example to demonstrate the process of calculating partial derivative by back propagation

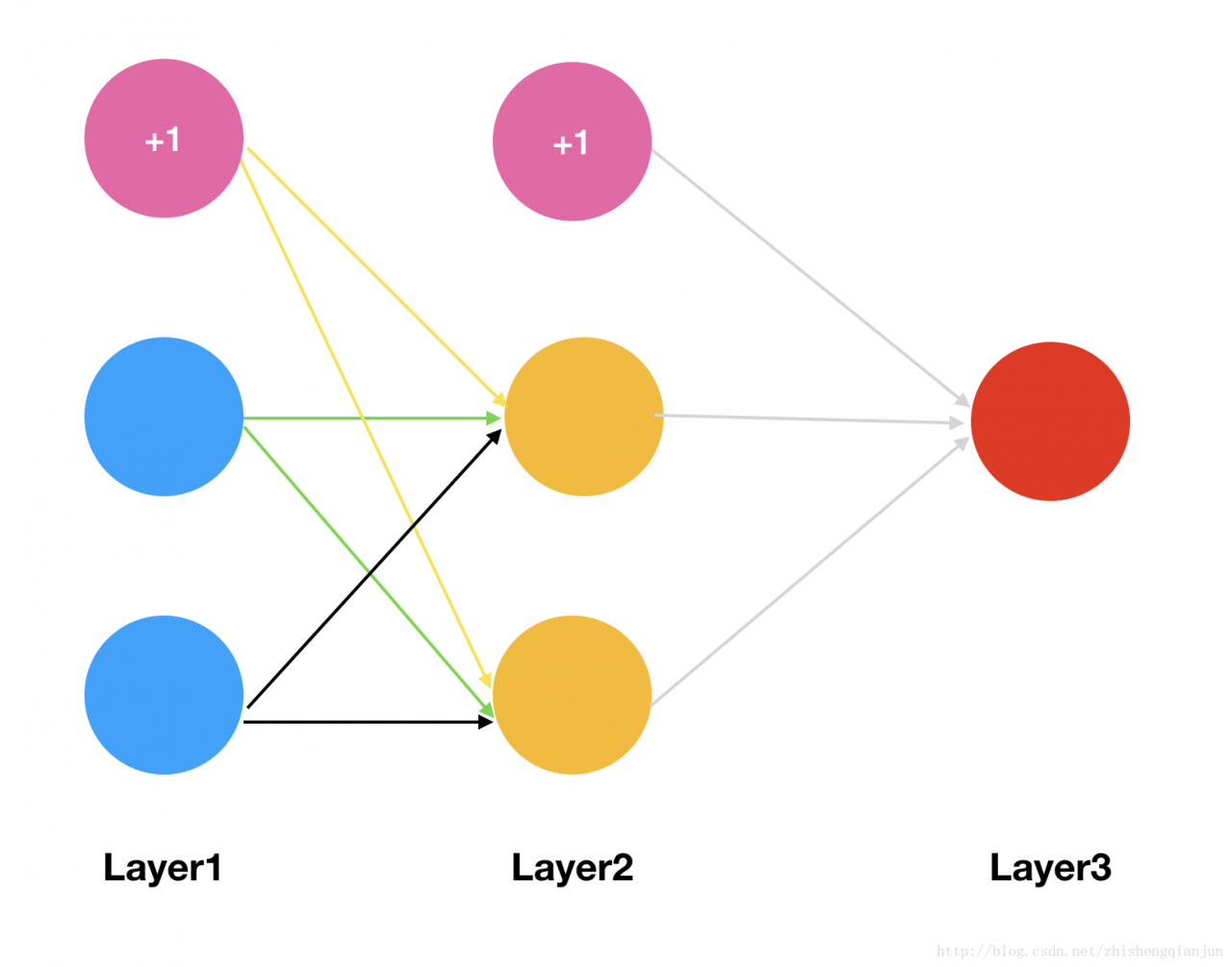
Then we will have two initial weight matrices:

θ1=[θ110θ120θ111θ121θ112θ122]θ2=[θ210θ211θ212]

We got the matrix above, and now we’re using

sigmoid

Function as the activation function to calculate the excitation of each layer of the network (assuming that we have only one sample, the input is

x1,x2,

The output is

y

）；

The first level is input, and the incentive is the eigenvalue of the sample

a1=⎡⎣⎢⎢x0x1x2⎤⎦⎥⎥

​

x0

Is the bias term, which is 1

The second layer is the hidden layer. The excitation is obtained by multiplying the eigenvalue with the region, and then the sigmoid function is used to transform the region

a2

Before transformation

z2

：

z21z22z2a2a2=θ110∗x0+θ111∗x1+θ112∗x2=θ120∗x0+θ121∗x1+θ122∗x2=[z21z22]=sigmoid(z2)=⎡⎣⎢⎢⎢1a21a22⎤⎦⎥⎥⎥

In the above, we add a bias term at the end;

Next, the third layer is the output layer

z31z3a3a3=θ210∗a20+θ211∗a21+θ212∗a22=[z31]=sigmoid(z3)=[a31]

Because it is the output layer, there is no need to calculate further, so the bias term is not added;

The above calculation process, from input to output, is also called forward propagation.

Then, we write the formula of the loss function according to the loss function. Here, there is only one input and one output, so the loss function is relatively simple

Here, M = 1;
1

J(Θ)=−1m[y(i)klog((hΘ(x(i)))k)+(1−y(i)k)log(1−(hΘ(x(i)))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2=−1m[y∗log(a3)+(1−y)∗log(1−a3)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2

Note:

λ2m∑L−1l=1∑sli=1∑sl+1j=1(Θ(l)j,i)2

In fact, it is the sum of squares of all the weights. Generally, the one multiplied by the offset term will not be put in. This term is very simple. Ignore it for the time being, and do not write this term for the time being (this is regularization).

​

J(Θ)=−1m[y∗log(a3)+(1−y)∗log(1−a3)]

Then we get the above formula, and here we know if we want to ask for it

θ212

If we use the partial derivative of, we will find that this formula is actually a composite function,

y

It’s a constant. A3 is a constant

z3

Of

sigmoid

Function transformation, and

z3

then is

a2

Now that we have found where the weight is, we can start to find the partial derivative,

a3

finish writing sth.

s(z3)

Then, we get the following derivation:

∂J(Θ)∂θ212=−1m[y∗1s(z3)−(1−y)∗11−s(z3)]∗s(z3)∗(1−s(z3))∗a212=−1m[y∗(1−s(z3)−(1−y)∗s(z3)]∗a212=−1m[y−s(z3)]∗a212=1m[s(z3)−y]∗a212=1m[a3−y]∗a212

According to the above derivation, we can get the following formula:
1

∂J(Θ)∂θ210∂J(Θ)∂θ211=1m[a3−y]∗a210=1m[a3−y]∗a211

So, remember what I said earlier, we will seek the derivative from top to bottom and save the partial derivative of the current multiple subunits. According to the above formula, we know that the partial derivative of the second weight matrix can be obtained by

[a3−y]

It is obtained by multiplying the excitation of the previous layer of network and dividing it by the number of samples, so sometimes we call the difference as

δ3

Then, the partial derivatives of the second weight matrix are obtained by multiplying them in the form of matrix;

Now that we have obtained the partial derivatives of the second weight matrix, how can we find the partial derivatives of the first weight matrix?

For example, we’re going to

θ112

Partial derivation:
0

∂J(Θ)∂θ112=−1m[y∗1s(z3)−(1−y)∗11−s(z3)]∗s(z3)∗(1−s(z3))∗θ211∗s(z2)∗(1−s(z2))∗x2=−1m∗[a3−y]∗θ211∗s(z2)∗(1−s(z2))∗x2=−1m∗δ3∗θ211∗s(z2)∗(1−s(z2))∗x2

From the formula on the line, we can see that the derivative we saved can be directly multiplied. If there is a multi-layer network, in fact, the following process is the same as this one, so we get the formula:
if there is a multi-layer network, the following process is the same as this one

δ3δ2=a3−y=δ3∗(θ2)T∗s(z2)′

Because this network is three layers, so we can get all the partial derivatives. If it is multi-layer, the principle is the same. Multiply it continuously. Starting from the second formula, the following forms are the same.

“Typeerror: invalid dimensions for image data” in Matplotlib drawing imshow() function

The key to solve this problem is to understand the parameters of imshow function. matplotlib.pyplot.imshow () the input of the function needs to be a two-dimensional numpy or a three-dimensional numpy of 3 or 4. When the depth of the third dimension is 1, use np.squeeze The () function compresses data into a two-dimensional array. Because I use it in the python environment, the output of the result is (batch)_ Size, channel, width, height), so I first need the detach() function to cut off the backpropagation. It should be pointed out that imshow does not support the display of tensors, so I need to use the. CPU () function to transfer to the CPU. As mentioned earlier, the input of imshow function needs to be a two-dimensional numpy or a three-dimensional numpy of 3 or 4, because my usage is quite special, and there is an additional batch_ Size dimension, but it’s OK. I set up batch_ The size is only 1. At this time, you can use the. Squeeze() function to remove 1 and get a (channel, width, height) numpy, which obviously does not meet the input requirements of imshow. Therefore, we need to use the transpose function to move channel (= 3) to the end, which is why we have the usage of. Transpose (1,2,0). Of course, if the image to be displayed itself is channel = 1, you can use the squeeze() function to get rid of it and directly input it to the imshow function as a two-dimensional numpy

plt.imshow(img2.detach().cpu().squeeze().numpy().transpose(1,2,0))

 

tf.gradients is not supported when eager execution is enabled. Use tf.GradientTape instead.

After learning Chapter 5 of deep learning with Python, deeply learn the thermodynamic diagram for computer vision
5.4.3 visualization class activation
when running the code in tensorflow 2.0 environment

grads = K.gradients(african_elephant_output, last_conv_layer.output)[0]

replace with

grads = tf.keras.backend.gradients(african_elephant_output, last_conv_layer.output)[0]

The following errors still occur

tf.gradients is not supported when eager execution is enabled. Use tf.GradientTape instead.

Solution

with tf.GradientTape() as gtape:
    grads = gtape.gradient(african_elephant_output, last_conv_layer.output)

Full code reference

reference resources:

https://stackoverflow.com/questions/58322147/how-to-generate-cnn-heatmaps-using-built-in-keras-in-tf2-0-tf-keras

The principle of deformable convolution

The concept of     deformable convolution was proposed in the paper: deformable convolutional networks
in this paper    as the name suggests, deformable convolution is derived from the concept of standard convolution. In standard convolution operation, the convolution core’s action area is always in the rectangular area of the size of the standard convolution core around the center point (as shown in figure a below), while deformable convolution can be an irregular area (as shown in Figure B, C, D below, where the offset of B is random; C, D are special cases).

The implementation method of     deformation convolution is shown in the following figure:

The dimension information of each part is as follows:
     input feature map: (batch, h, W, c)
    output feature map: (batch, h, W, n)
    offset field: (batch, h, W, 2n)
     offset field is obtained by standard convolution operation on the original graph, and the number of channels is 2n, which means n 2-dimensional offsets

（

△

x

，

△

y

）

（△x，△y）

(△ x, △ y), n is the number of convolution kernels, that is, the number of channels of output characteristic layer. The process of deformation convolution can be described as follows: firstly, standard convolution is performed on the input feature map to obtain n 2-dimensional offsets

（

△

x

，

△

y

）

（△x，△y）

(△ x, △ y), and then modify the values of each point on the input feature map (let feature map be

P

P

P. Namely

P

（

x

，

y

）

=

P

（

x

+

△

x

，

y

+

△

y

）

P（x，y）=P（x+△x，y+△y）

P (x, y) = P (x + △ x, y + △ y), when

x

+

△

x

x+△x

When x + △ x is a fraction, bilinear interpolation is used

P

（

x

+

△

x

，

y

+

△

y

）

P（x+△x，y+△y）

P（x+△x，y+△y））。 Form n feature maps, and then use n convolution kernels to convolute one by one to get the output.
The calculation results of   standard convolution and deformation convolution are shown in the following figure:

Summary of Python deep learning packages

Python deep learning often uses package summaries
Update history

2021/2/28

1.pytorch
Website: https://pytorch.org/
Current installed version: 1.7.1

pip install torch===1.7.1+cu110 torchvision===0.8.2+cu110 torchaudio===0.7.2 -f https://download.pytorch.org/whl/torch_stable.html

2. scikit-learn(sklearn)

pip install scikit-learn

Current version: 0.24.1
3.pandas

pip install pandas

Current version: 1.2.2
Installing Pandas will install Numpy
4.numpy

pip install numpy

Current version: 1.20.1

Previous installers of PyTorch did not use the latest Numpy. 1.16.6 does.
But now the latest version does.

5.matplotlib

pip install matplotlib

Current version: 3.3.4
6 tensorflow 1.15

pip install tensorflow==1.15 -i http://pypi.douban.com/simple/

Less use of
1.networkx
NetworkX is a Python package for building and manipulating complex graph structures and providing algorithms for analyzing graphs.

pip install networkx

Current version: 2.5

ValueError: need at least one array to concatenate

keywords
python
Content of the error
ValueError: need at least one array to concatenate
why
Wrong path
Possible places to start
1. Check the path written in the running py file
2. If you are a PyCharm remote connection, it is recommended to check whether “Automatic synchronization to the server” is enabled (open method: Tools — Deployment — Automatic Upload).

Build your own resnet18 network and load torch vision’s own weight 

import torch
import torchvision
import cv2 as cv
from utils.utils import letter_box
from model.backbone import ResNet18


model1 = ResNet18(1)
model2 = torchvision.models.resnet18(progress=False)
fc = model2.fc
model2.fc = torch.nn.Linear(512, 1)
# print(model)
model_dict1 = model1.state_dict()
model_dict2 = torch.load('resnet18.pth')
model_list1 = list(model_dict1.keys())
model_list2 = list(model_dict2.keys())
len1 = len(model_list1)
len2 = len(model_list2)
minlen = min(len1, len2)
for n in range(minlen):
    if model_dict1[model_list1[n]].shape != model_dict2[model_list2[n]].shape:
        continue
    model_dict1[model_list1[n]] = model_dict2[model_list2[n]]

model1.load_state_dict(model_dict1)
missing, unspected = model2.load_state_dict(model_dict2)
image = cv.imread('zhn1.jpg')
image = letter_box(image, 224)
image = image[:, :, ::-1].transpose(2, 0, 1)
print('Network loading complete.')
model1.eval()
model2.eval()
with torch.no_grad():
    image = torch.tensor(image/256, dtype=torch.float32).unsqueeze(0)
    predict1 = model1(image)
    predict2 = model2(image)
print('finished')
# torch.save(model.state_dict(), 'resnet18.pth')

Runtimeerror using Python training model: CUDA out of memory error resolution

RuntimeError: CUDA out of memory occurs using the PyTorch training model
Training: Due to the limited GPU video memory resources, the batchsize of training input should not be too large, which will lead to Out of Memory errors.
Solution: Reduce the batchSize to even 1
Use with torch.no_grad():fore testing the code