Sigmoid function is a mathematical function with beautiful S-shape curve, which is widely used in logistic regression and artificial neural network. The mathematical form of sigmoid function is:
0

f(x)=11+e−x

The function image is as follows:

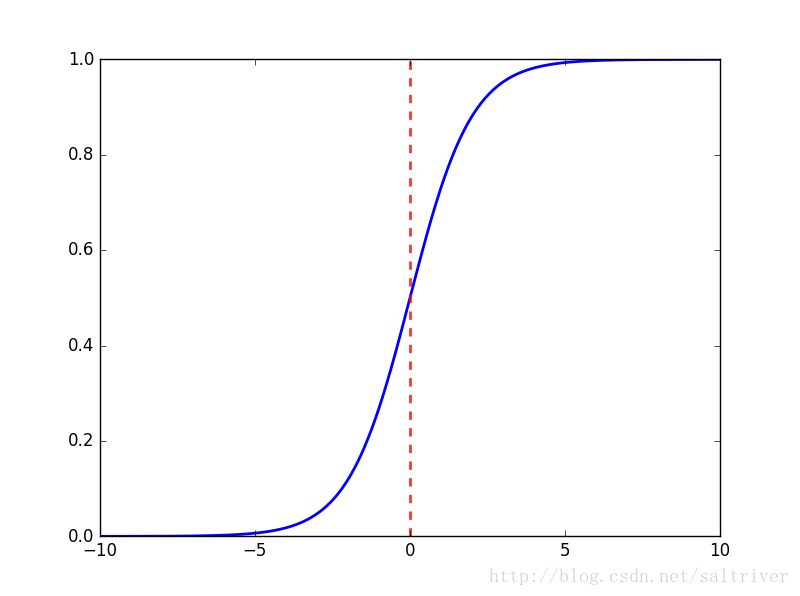
It can be seen that sigmoid function is continuous, smooth, strictly monotone, and symmetric with (0,0.5) center, which is a very good threshold function.

When x approaches negative infinity, y approaches 0; when x approaches positive infinity, y approaches 1; when x = 0, y = 0.5. Of course, when x goes beyond the range of [- 6,6], the value of the function basically does not change, and the value is very close, so it is generally not considered in the application.

The range of sigmoid function is limited between (0,1). We know that [0,1] corresponds to the range of probability value, so sigmoid function can be associated with a probability distribution.

The derivative of sigmoid function is its own function, that is

f′(x)=f(x)(1−f(x))

The calculation is very convenient and time-saving. The derivation process is as follows:
according to the commonly used derivation formula,
is obtained

f′(x)=(−1)(1+e−x)−2(0+(−1)e−x)=e−x(1+e−x)2=e−x1+e−x11+e−x

And:

1−f(x)=1−11+e−x=e−x1+e−x

Therefore,

f′(x)=f(x)(1−f(x))

.

Although sigmoid function has good properties, it can be used in classification problems, such as the classifier of logistic regression model. But why choose this function? In addition to the above mathematical easier to deal with, there are its own derivation characteristics.
For the classification problem, especially for the binary classification problem, it is assumed that the distribution obeys Bernoulli distribution. The PMF of Bernoulli distribution is:
0

f(x|p)=px(1−p)1−x

According to《

The general expression framework of the family of exponential distributions is as follows

f(x|θ)=h(x)exp{η(θ)T(x)−A(θ)}

The Bernoulli distribution is transformed into:

f(x|p)=exp{ln(p1−p)x+log(1−p)}

Among them:

θ=p

，

h(x)=1

，

T(x)=x

，

η(θ)=lnp1−p

，

A(θ)=−ln(1−p)

. Therefore, Bernoulli distribution also belongs to exponential distribution family.

We can deduce it

p

And η (θ):
the relationship between η (θ) and η (θ) was analyzed

η(θ)=lnp1−p

Then:

−η(θ)=−lnp1−p=ln1−pp=ln(1p−1)

The results are as follows

e−η(θ)=1p−1

1+e−η(θ)=1p

p=11+e−η(θ)

This is the form of sigmoid function.